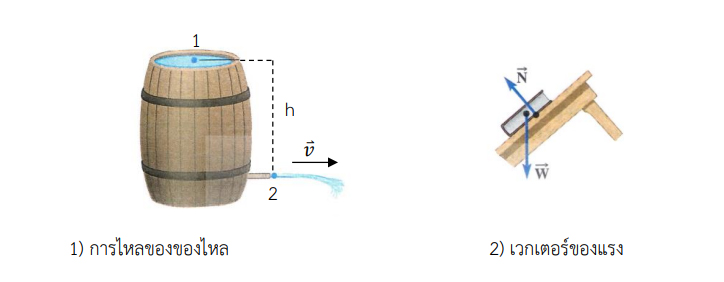
เรื่องเวกเตอร์-ปริภูมิเวกเตอร์ (Vector space)
ปริภูมิเวกเตอร์
บ้านของเวกเตอร์เรียกว่าปริภูมิเวกเตอร์ (vector space) มักจะแทนด้วยตัวอักษร V บ้านในที่นี้หมายถึงคนในบ้านมากกว่าบ้านเลขที่ เหมือนคำกล่าวที่ว่าประเทศคือประชาชน ไม่ใช่เขตแดน ปริภูมิเวกเตอร์เป็นเซตของวัตถุที่ทำตามกฏหนึ่ง กฏก็คือเมื่อคุณวัตถุด้วยตัวเลข (ซึ่งเลือกได้ เช่นจะให้เป็นจำนวนจริงหรือจำนวนเชิงซ้อน แต่เมื่อเลือกแล้วจะเปลี่ยนไม่ได้) หรือเอาวัตถุไปรวมกับวัตถุอื่นในเซต ผลที่ออกมาจะไม่ออกนอกเซต ไม่ออกนอกบ้าน วัตถุที่ทำตามกฏนี้เรียกว่าเวกเตอร์ จำไว้ว่าการคูณด้วยตัวเลขกับการบวกกันเองเป็นการการกระทำการพื้นฐานที่ทำได้กับเวกเตอร์
อาจจะมีเวกเตอร์จำนวนอนันต์อยู่ในบ้านหลังหนึ่ง ไอเดียที่สำคัญก็คือเราสามารถเลือกเวกเตอร์หยิบมือหนึ่งมาเป็นตัวแทนของทุกเวกเตอร์ได้ เราเรียกเซตของเวกเตอร์นี้ว่าฐานหรือเบสิส (basis) เหมือนรากฐานของบ้าน มีฐานก็ต่อเป็นบ้านได้ สมาชิกของเซตนี้เราเรียกว่าเวกเตอร์ฐาน (basis vector) ฐานเป็นตัวแทนของทุกๆเวกเตอร์ในบ้านเพราะนิยามดังต่อไปนี้
- ไม่ว่าเราจะเลือกเวกเตอร์ไหนในบ้าน เราสามารถเขียนมันในรูปผลรวมของเวกเตอร์ที่มาจากการจับสมาชิกในฐานคูณกับตัวเลขได้ ผลรวมนี้มีชื่อเป็นทางการว่าผลรวมเชิงเส้น (linear combination) (เชิงเส้นเพราะไม่มีการยกกำลัง)
- ผลรวมเชิงเส้นที่ต่างกันเป็นตัวแทนของเวกเตอร์ที่ต่างกัน
จากสองข้อกำหนดนี้เราสามารถพิสูจน์ได้ว่าถึงแม้จะมีหลายเซตที่ใช้เป็นฐานของบ้านได้ แต่ทุกๆเซตจะมีจำนวนสมาชิกเท่ากัน เราเรียกจำนวนนี้ว่ามิติ (dimension) ซึ่งมักจะแทนด้วยตัวอักษร d คำว่ามิตินี้ตรงกับความหมายของคำว่ามิติเมื่อเรามองเวกเตอร์เป็นลูกศร ทำให้คิดถึงปริภูมิเวกเตอร์ในเชิงเรขาคณิตได้
ปริภูมิย่อย (subspace) เป็นบ้านที่อยู่ในบ้านอีกที เช่นเส้นตรง (หนึ่งมิติ) อยู่ในระนาบ (สองมิติ) ซึ่งอยู่ในปริภูมิสามมิติ กว้าง, ยาว, สูงอีกที ในสัมพัทธภาพพิเศษก็มีมิติเวลาเพิ่มมาอีกหนึ่งมิติ
แต่มิติไม่จำเป็นต้องมีความเกี่ยวข้องมิติทางกายภาพ ในสถิติ, machine learning, หรือทฤษฎีควอนตัมเราสามารถมีข้อมูลเป็นเวกเตอร์ในมิติสูงๆได้ ใครที่อยากทำเรื่องพวกนี้ก็ต้องใช้เวกเตอร์ทั้งนั้น
บางครั้งเราก็ต้องการเซตของเวกเตอร์ที่ใหญ่กว่าฐาน เวกเตอร์ใดๆก็ยังเขียนในรูปผลรวมเชิงเส้นของเซตนี้ได้ เราใช้คำว่าเซ็ตนี้แผ่ทั่ว (span) ปริภูมิหรือเซตนี้เป็น spanning set เพียงแค่ว่าเวกเตอร์หนึ่งอาจจะมีได้หลายตัวแทน (คือตัดข้อสองในนิยามด้านบนออกไป)
พีชคณิตเวกเตอร์ (Vectors algebra)
ในทางฟิสิกส์และวิศวกรรมศาสตร์นั้นการทราบจำนวนและหน่วยของปริมาณใดปริมาณหนึ่งจะไม่เพียงพอสำหรับอธิบายปริมาณนั้น ๆ ให้สมบูรณ์ได้ เช่น การเดินไปทางทิศเหนือ 8 กิโลเมตร ย่อมมีตำแหน่งแตกต่างจากการเดินไปทางทิศตะวันออก 6 กิโลเมตร การกล่าวเพียงสั้น ๆ ว่าได้เดินทางไป 8 กิโลเมตร จะไม่สามารถบอกตำแหน่งสุดท้ายได้ถ้าไม่ทราบทิศของการเดิน ตำแหน่งที่เปลี่ยนไปนี้เราเรียกว่า การกระจัด (Displacement) ซึ่งเรียกปริมาณที่มีทั้งขนาด (Magnitude) และทิศทาง (Direction) ว่า ปริมาณเวกเตอร์ (Vector quantity) เช่น ความเร็ว ความเร่ง แรง โมเมนต์ ฯลฯ ส่วนปริมาณที่มีเฉพาะขนาดเพียงอย่างเดียวจะเรียกว่า ปริมาณสเกลาร์ (Scalar quantity) เช่น มวล ปริมาตร ความหนาแน่น ความดัน อุณหภูมิ อัตราเร็ว อัตราเร่ง ฯลฯ การคำนวณทางคณิตศาสตร์ของปริมาณสเกลาร์ จะเหมือนกับการคำนวณทั่วไป ส่วนการคำนวณปริมาณเวกเตอร์ จะต้องคำนึ่งถึงทิศทางของปริมาณนั้นด้วย จึงเรียกการคำนวณแบบนี้ว่า พีชคณิตเวกเตอร์ (Vector algebra) ซึ่งจะกล่าวอย่าง ละเอียดดังต่อไปนี้
1.1.1 ปริมาณสเกลาร์ (Scalar quantity) ปริมาณสเกลาร์ คือ ปริมาณที่มีแต่ขนาดเพียงอย่างเดียว ไม่มีทิศทาง ตัวอย่าง เช่น เวลา อุณหภูมิประจุไฟฟ้า พลังงาน และปริมาตร มวล ระยะทาง อัตราเร็ว อัตราเร่ง เป็นต้น ดังนั้นปริมาณสเกลาร์จึงเป็นปริมาณต่าง ๆ ที่บอกแต่เพียงขนาดเพียงอย่างเดียวก็เป็นที่เข้าใจได้อย่างสมบูรณ์ได้
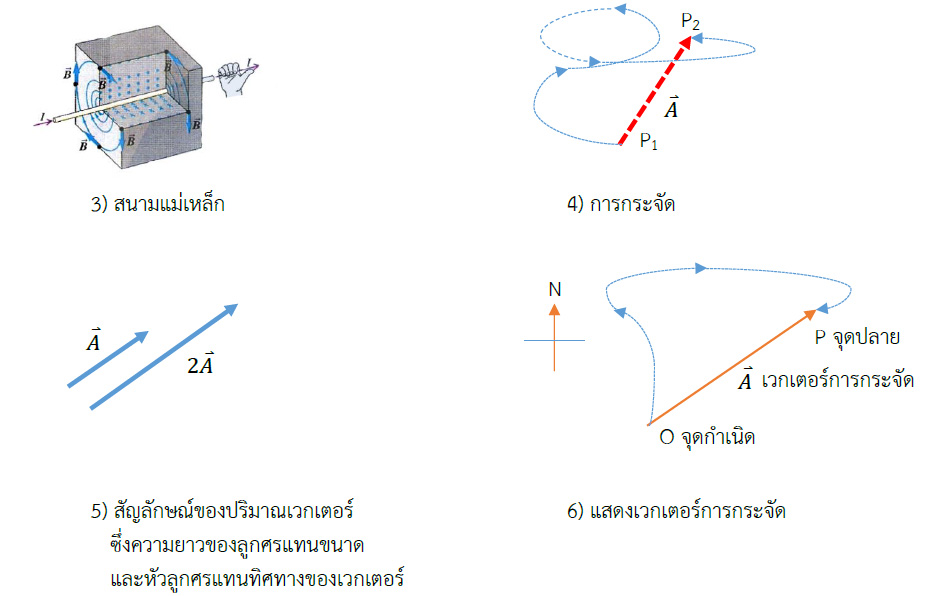
1.1.2 ปริมาณเวกเตอร์ (Vector quantity) ปริมาณเวกเตอร์ คือ ปริมาณที่มีทั้งขนาดและทิศทาง ซึ่งอาจเขียนแทนด้วยลูกศร โดยความยาวลูกศรจะแสดงขนาดและหัวลูกศรแสดงทิศทางของเวกเตอร์นั้น ๆ นอกจากนี้เรายังสามารถเขียนเวกเตอร์ได้ โดยการกำหนดขนาดเวกเตอร์ด้วยตัวอักษรโรมันที่มีหัวลูกศรกำกับ
หรือเขียนเป็นตัวตัวหนา (ตัวทึบ) ก็ได้ ดังเช่นรูปที่ 1-6 ( ในเอกสารนี้จะใช้สัญลักษณ์ A แทนเวกเตอร์ 𝐴⃑ หรือ 𝐵 แทนเวกเตอร์ 𝐵⃑ )