ในคณิตศาสตร์ เพาเวอร์เซต (Power set) ของเซต $A$ คือเซตของทุกเซตย่อยของ $A$ เขียนแทนด้วย $\mathcal{P}(A)$

ตัวอย่างเช่น หาก A=1,2,3 เพาเวอร์เซตของ $A$ คือ $\mathcal{P}(A) = \\{\\{\}, \\{1\\}, \\{2\\}, \\{3\\}, \\{1, 2\\}, \\{1, 3\\}, \\{2, 3\\}, \\{1, 2, 3\\}\\}$

เพาเวอร์เซตของเซต $A$ เสมอมีขนาดใหญ่กว่าเซต $A$ เสมอ ตัวอย่างเช่น เพาเวอร์เซตของเซต $\{1,2\}$ มีสมาชิก 4 คน ในขณะที่เซต $\{1,2\}$ มีสมาชิก 2 คน

เพาเวอร์เซตของเซต $A$ สามารถสร้างขึ้นได้ด้วยวิธีการดังนี้

1. เริ่มจากเซต $A$
2. พิจารณาทุกเซตย่อยของ $A$
3. รวมทุกเซตย่อยของ $A$ เข้าด้วยกัน

เพาเวอร์เซตของเซต $A$ มักใช้เพื่อศึกษาความสัมพันธ์ระหว่างเซตต่างๆ

สับเซต และ เพาเวอร์เซต

สับเซต (subset) หรือ “เซตย่อย”  คือ เซตที่เล็กกว่าหรือเท่ากันกับเซตที่กำหนด โดยต้องใช้สมาชิกร่วมกับเซตที่กำหนดเท่านั้น

            สัญลักษณ์ที่ใช้แทนประโยค “ A เป็นสับเซตของ B” คือ A Ì B และจะเกิดขึ้นได้ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A นั้นเป็นสมาชิกของเซต B ด้วย หรือเมื่อ A เป็นเซตว่างก็ได้

เช่น {1,2}Ì{1,2,3}เนื่องจากทั้ง 1 และ 2 เป็นสมาชิกของ {1,2,3}

รูปแบบ เซต (เล็ก) Ì เซต(ใหญ่)

สมบัติของซับเซต

1. A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2. A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3. Ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4. ถ้า A ⊂ ø แล้ว A = ø

5. ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6. A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7. ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

การหาสับเซตทั้งหมดของA

จำนวนสับเซตทั้งหมดหาได้จาก 2ⁿ เมื่อ n = จำนวนสมาชิกในเซต

ตัวอย่าง             จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}

A จะมีสับเซตทั้งหมด 2⁴ =16 สับเซต เมื่อแจกแจงสับเซตทั้งหมดจะได้ดังนี้

Ø

{2}  {4}  {6}  {8}

{2, 4}  {2, 6}  {2, 8}  {4, 6}  {4, 8}  {6, 8}

{2, 4, 6}  {2, 6, 8}  {2, 4, 8}  {4, 6, 8}

{2, 4, 6, 8}

ความหมายของสับเซตแท้

สับเซตแท้ คือ สับเซตทั้งหมดที่ไม่ใช่ตัวมันเอง มี 2ⁿ – 1 สับเซต (เซตว่างไม่มีสับเซตแท้)

นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B

ซึ่งจะได้รูปดังภาพ

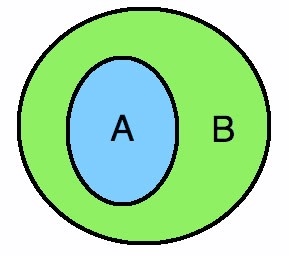
การหาจำนวนสับเซตทั้งหมดของ A

            หลักในการเขียนสับเซตทั้งหมดของเซตๆหนึ่งที่โจทย์กำหนดมาทำโดย เริ่มเขียนตั้งแต่เซตว่าง แล้วตามด้วยเซตที่มีสมาชิก 1 ตัว, 2 ตัว ไปเรื่อยๆ จนมีสมาชิกเท่ากับเซตที่โจทย์กำหนดมา (ตัวมันเอง) โดยสมาชิกที่นำมาใช้เขียนต้องเป็นสมาชิกของเซตที่โจทย์กำหนดมาด้วย

ตัวอย่าง  จงเขียนสับเซตทั้งหมดของเซตต่อไปนี้

1. A = Ø สับเซตทั้งหมดของ A มี 1 สับเซต คือ Ø

2. B = {1} สับเซตทั้งหมดของ B มี 2 สับเซต คือ 1) Ø   2) {1}

3. C = {1,3} สับเซตทั้งหมดของ C มี 4สับเซต คือ  1) Ø   2) {1}  3) {3}   4) {1,3}

4. D = {1,3,5} สับเซตทั้งหมดของ D มี 4 สับเซต คือ1) Ø   2) {1}   3) {3}   4) {5}   5) {1,3}   6)  

   {1,5}   7) {3,5}   8) { 1,3,5}

 

เซต	จำนวนสมาชิกของเซต	จำนวนสับเซตทั้งหมด
1. A = Ø  2. B = { 1 }  3. C = { 1 , 3 }  4. D = { 1 , 3 , 5 }	0 1 2 3	20 = 1 21 = 2 22 = 4 23 = 8

จากตาราง พิจารณาความสัมพันธ์ของสมาชิกของเซตกับจำนวนสับเซตทั้งหมดจะได้ว่า

จำนวนสับเซตทั้งหมดของเซต A = 2^n(A)

จำนวนสับเซตแท้ทั้งหมดของ A

นิยาม : สับเซตแท้ (proper set) ของ A คือ สับเซตทั้งหมดของเซต A ยกเว้น ตัวมันเอง (ยกเว้น A)

1.มีเซตอะไรไหมที่ไม่มีสับเซตแท้
ตอบ มี เซตดังกล่าวคือเซตว่าง เพราะว่าสับเซตของ Ø ก็คือ Ø เพียงตัวเดียว ดังนั้น เซตว่างจึงไม่มีสับเซต

         แท้

2. จำนวนสับเซตแท้ของเซต A = 2^n(A)  -1   สับเซต

โจทย์ประยุกต์ เรื่อง สับเซต

 

ข้อ1. ถ้า A={a, b,c,d,e,f} และ B={a,b} แล้วจำนวนเซต X ซึ่ง   B⊂X⊂A เท่ากับข้อใดต่อไปนี้

1.4                                2.15                              3.16                              4.32

เฉลย.

B⊂Xแปลว่า a, b ต้องอยู่ใน X ซึ่ง X⊂Aแปลว่า c, d, e, f อยู่ใน X กี่ตัวก็ได้

∴จำนวนแบบที่เป็นไปได้ของ X ก็คือจำนวนสับเซตทุกแบบของ {c, d, e, f}

นั่นคือ 2^4=16 แบบ

ข้อ2. ถ้า A={5, 6, 7, …,20} และ B={1, 2, 3,…,15} แล้ว จำนวนสมาชิกในเซต {X | X เป็นสับเซตของ A และ X ไม่เป็นสับเซตของ B}

 

1. (7×2)^10                                                      2. (31×2)^11

3. (31×2)^10                                                    4. (63×2)^11

เฉลย.

คิดโดยวิธีลบออก คือ จำนวนสับเซตของ A ทุกแบบ ลบออกด้วยแบบที่เป็นสับเซตของ  B ด้วย

จะได้เท่ากับ 2^16-2^11=31×2^11