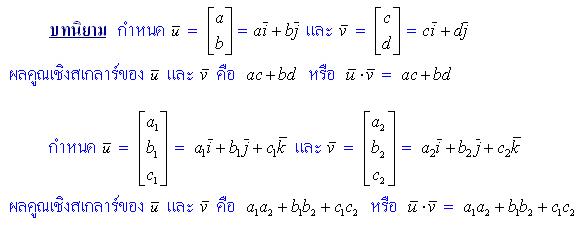สเกลาร์และเวคเตอร์ (Scalar and Vector)

1.1.1 ปริมาณสเกลาร์ (Scalar quantity) ปริมาณสเกลาร์ คือ ปริมาณที่มีแต่ขนาดเพียงอย่างเดียว ไม่มีทิศทาง ตัวอย่าง เช่น เวลา อุณหภูมิประจุไฟฟ้า พลังงาน และปริมาตร มวล ระยะทาง อัตราเร็ว อัตราเร่ง เป็นต้น ดังนั้นปริมาณสเกลาร์จึงเป็นปริมาณต่าง ๆ ที่บอกแต่เพียงขนาดเพียงอย่างเดียวก็เป็นที่เข้าใจได้อย่างสมบูรณ์ได้
1.1.2 ปริมาณเวกเตอร์ (Vector quantity) ปริมาณเวกเตอร์ คือ ปริมาณที่มีทั้งขนาดและทิศทาง ซึ่งอาจเขียนแทนด้วยลูกศร โดยความยาวลูกศรจะแสดงขนาดและหัวลูกศรแสดงทิศทางของเวกเตอร์นั้น ๆ นอกจากนี้เรายังสามารถเขียนเวกเตอร์ได้ โดยการกำหนดขนาดเวกเตอร์ด้วยตัวอักษรโรมันที่มีหัวลูกศรกำกับ
หรือเขียนเป็นตัวตัวหนา (ตัวทึบ) ก็ได้ ดังเช่นรูปที่ 1-6 ( ในเอกสารนี้จะใช้สัญลักษณ์ A แทนเวกเตอร์ 𝐴⃑ หรือ 𝐵 แทนเวกเตอร์ 𝐵⃑ )

ปริมาณทางฟิสิกส์ที่ส าคัญมีอยู่ 2 อย่าง คือ ปริมาณสเกลาร์ และ ปริมาณเวคเตอร์ ปริมาณสเกลาร์(Scalar) คือ ปริมาณที่มีขนาดเพียงอย่างเดียว เช่น มวล (mass),ความยาว (length), เวลา (time), อุณหภูมิ (temperature), ปริมาตร (volume)ปริมาณเวคเตอร์(Vector) คือ ประมาณที่มีทั้งขนาดและทิศทาง เช่น การกระจัด (displacement), แรง (Force), ความเร็ว (Velocity), ความเร่ง (Acceleration),

พีชคณิตของเวคเตอร์ (Vector Algebra)

พีชคณิตเวกเตอร์ (Vectors algebra)

พีชคณิตเวกเตอร์ (Vectors algebra) ในทางฟิสิกส์และวิศวกรรมศาสตร์นั้นการทราบจํานวนและหน่วยของปริมาณใดปริมาณหนึ่งจะไม่เพียงพอ สําหรับอธิบายปริมาณนั้น ๆ ให้สมบูรณ์ได้เช่น การเดินไปทางทิศเหนือ 8 กิโลเมตร ย่อมมีตําแหน่งแตกต่างจาก
การเดินไปทางทิศตะวันออก 6 กิโลเมตร การกล่าวเพียงสั้

พืชคณิตเวกเตอร์ ( vector Algebra )

  เวกเตอร์คือปริมาณที่มีท้ั้งขนาดและทิศทาง เวกเตอร์มีประโยชน์ในการศึกษาทางวิทายาศาสตร์โดยเฉพาะวิชาฟิสิกส์ เช่น แรง ความเร็ว ความเร่ง ในบทนี้จะกล่าวถึงพีชคณิตเวกเตอร์ เช่น การบวกเวกเตอร์ การลบเวกเตอร์ การคูณเวกเตอร์ มุมระหว่างเวกเตอร์ ผลคูณของสามเวกเตอร์ เป็นต้น

1.1 พิกัดฉากในปริภูมิสามมิติ

         ระบบแกนพิกัดฉากในปริภูมิสามมิติ เป็นระบบที่ประกอบด้วยเส้นตรงสามเส้นตั้งฉากซึ่งกันและกัน ตัดกันที่จุดกำเนิด 0 เส้นตรงทั้งสามเรียกว่า แกน x แกน y  แกน z ดังรูปที่ 1.1

เวกเตอร์ (vector)

เวกเตอร์เป็นเครื่องมือทางคณิตศาสตร์อย่างหนึ่ง ซึ่งดูเหมือนไม่มีความจำเป็นแตเป็นเครื่องมืออย่างแรกที่ต้องใช้  อย่างไรก็ตามในการศึกษาทางฟิสิกส์เวกเตอร์เป็นเครื่องมือที่มีความสำคัญ  เพื่อช่วยในอำนวยความสะดวกในการคำนวณ

2.1      ระบบพิกัด (แกนอ้างอิง)

          ระบบพิกัดมีความสำคัญเพื่อช่วยในการวัดมีความหมาย  เช่นอีก 800 m ถึงอาคารวิทยาศาสตร์เป็นการบอกที่ไม่สมบูรณ์  เนื่องจากไม่ทราบว่าเริ่มต้นที่ตำแหน่งใด

          ดังนั้นในการกำหนดระบบพิกัดต้องทราบ

ก.     จุดเริ่มต้น

ข.     ชนิดของระบบพิกัด (พิกัดฉาก ; พิกัดเชิงขั้ว ; พิกัดทรงกระบอก)

ค.     ทิศตามแกน

ระบบพิกัดแบบมาตรฐานใน 2 มิติ

ได้แก่ระบบพิกัดฉาก (Cartesian)   และ    ระบบพิกัดเชิงขั้ว (Polar)

พีชคณิตเวกเตอร์ (Vectors algebra)

พีชคณิตเวกเตอร์ (Vectors algebra) ในทางฟิสิกส์และวิศวกรรมศาสตร์นั้นการทราบจํานวนและหน่วยของปริมาณใดปริมาณหนึ่งจะไม่เพียงพอ สําหรับอธิบายปริมาณนั้น ๆ ให้สมบูรณ์ได้เช่น การเดินไปทางทิศเหนือ 8 กิโลเมตร ย่อมมีตําแหน่งแตกต่างจาก
การเดินไปทางทิศตะวันออก 6 กิโลเมตร การกล่าวเพียงสั้

บทนิยาม  1  ถ้าเวกเตอร์  u และ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ แล้ว ผลบวกของเวกเตอร์  u และ v เขียนแทนด้วยเวกเตอร์  u + v  หาได้จากให้ตำแหน่งเวกเตอร์ v มีจุดเริ่มต้นอยู่ที่จุดสิ้นสุดของเวกเตอร์ u
เวกเตอร์ u + v  จะแทนด้วยลูกศรจากจุดเริ่มต้นของเวกเตอร์ u  ไปยังจุดสิ้นสุดของเวกเตอร์  v ดังรูปที่  2

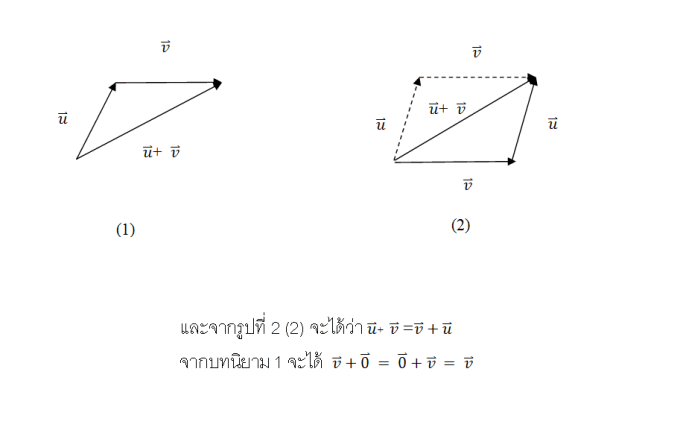(รูปที่ 2)

บทนิยาม 2 ให้เวกเตอร์ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ และ k เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ แล้ว เวกเตอร์  kv หมายถึงเวกเตอร์ที่มีขนาดเท่ากับ |k| เท่าของเวกเตอร์ v เมื่อ k>0 เวกเตอร์ kv จะมีทิศทางเดียวกับ v และเมื่อ k<0 เวกเตอร์ kv มีทิศตรงข้ามกับเวกเตอร์ v และให้เวกเตอร์  kv =0 เมื่อ k =0

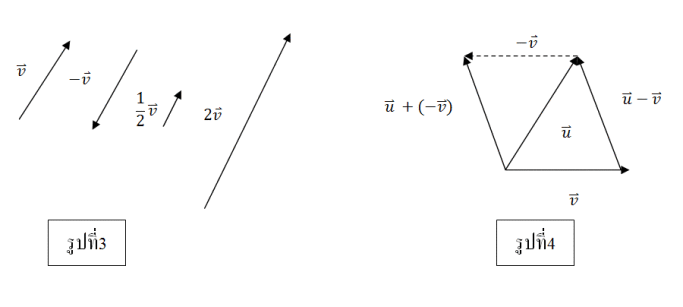จากรูปที่  3 ได้ว่าเวกเตอร์  v กับเวกเตอร์  Kv เป็นเวกเตอร์ที่ขนานกัน

สมบัติการบวกในระนาบ

1. u + v เป็นเวกเตอร์ในระนาบ สมบัติปิด
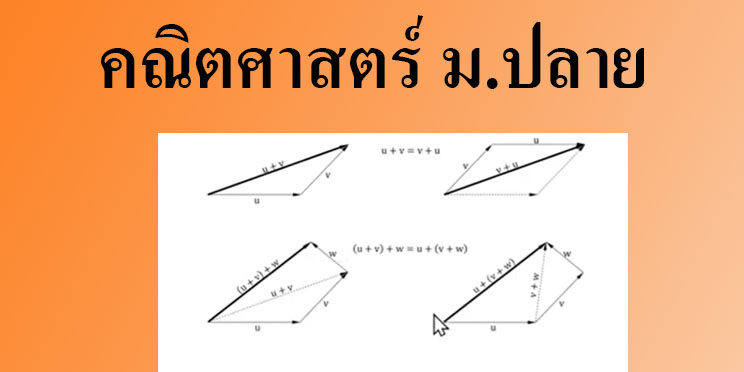
2. u + v = v + u สมบัติการสลับที่
3. u + (v + w) = (u + (v) + w สมบัติการเปลี่ยนกลุ่มได้
4. มี 0 โดยที่ 0 + u = u + 0 = u สมบัติการมีเอกลักษณ์
5. สำหรับทุก ๆ u จะมี -u โดยที่ -u + u = 0 = u + (-u) สมบัติการผกผัน
6. ถ้า u = v แล้ว w + v = w + u สมบัติการบวกด้วยเวกเตอร์ที่เท่ากัน

กราฟแสดงผลบวก u + v

ให้
u = ai + bj
v = ci + dj
u + v = (a + c)i + (b + d)j
u – v = (a – c)i + (b – d)j

เวกเตอร์ศูนย์

1. เวกเตอร์ศูนย์ 0 (0) คือเวกเตอร์ที่มีขนาดศูนย์หน่วย
2. จุดเริ่มต้นและจุดสิ้นสุดของเวกเตอร์ศูนย์เป็นจุดเดียวกัน

การคูณเวกเตอร์ด้วยสเกลาร์

ให้เวกเตอร์ u จะเขียน 2u ได้ 2u = u + u

สมบัติการคูณเวกเตอร์ด้วยสเกลาร์

ให้ u และ v เป็นเวกเตอร์ใด ๆ ในระนาบ a และ b เป็นจำนวนจริง
1. au เป็นเวกเตอร์ในระบบ สมบัติปิด
2. a(bu) = (ab)u สมบัติการเปลี่ยนกลุ่ม
3. (a + b)u = au + bu สมบัติการแจกแจง
4. a(u + v) = au + av สมบัติการแจกแจง
5. 1u = u
6. ถ้า au = 0 แล้ว a = 0 หรือ u = 0

เวกเตอร์หนึ่งหน่วย (Unit vector)

เวกเตอร์หนึ่งหน่วย คือ เวกเตอร์ที่มีขนาดเท่ากับ 1

มองภาพเห็นไหม ยกตัวอย่างให้เห็นภาพชัดเจน

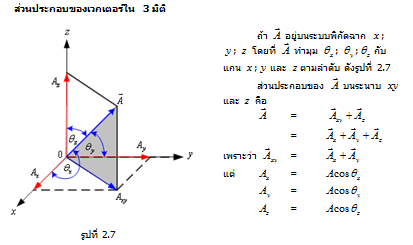
ส่วนประกอบของเวกเตอร์

เวกเตอร์หนึ่งหน่วย คือเวกเตอร์ที่มีขนาด 1 หน่วย และมีทิศทางตามเวกเตอร์ที่พิจารณา เช่น ให้ เป็นเวกเตอร์ที่มีขนาดเท่ากับ และ เป็นเวกเตอร์หนึ่งหน่วย ที่มีทิศเดียวกับเวกเตอร์ ดังรูป

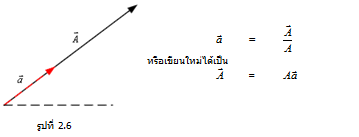
ดังนั้นในระบบพิกัดแกนมุมฉาก เวกเตอร์หนึ่งหน่วยแทนด้วย

มีขนาด 1 หน่วยทิศตามแกน X

มีขนาด 1 หน่วยทิศตามแกน Y

มีขนาด 1 หน่วยทิศตามแกน Z

โดยเวกเตอร์ทั้งสามตั้งฉากซึ่งกันและกัน และเวกเตอร์ทั้งสามจะเรียงกันในทิศทวนเข็มนาฬิกา

จากตัวอย่างที่ 2.3  คำตอบที่ได้สามารถเขียนใหม่ได้เป็น เป็นการเขียนในรูปแบบมาตรฐานซึ่งมีความสะดวกมากเมื่อนำไปใช้ในการบวกและการคูณเวกเตอร์

รูปแแบบทั่ว ๆ ไปของเวกเตอร์เขียนได้ดังนี้ เมื่อ คือส่วนประกอบบนแกน ของ  ; คือส่วนประกอบบนแกน ของ ; คือส่วนประกอบบนแกน ของ เป็นเวกเตอร์ใน 3 มิติ

เวกเตอร์หนึ่งหน่วย (Unit vector)

เวกเตอร์หนึ่งหน่วย (Unit vector)

ผลคูณเชิงสเกลาร์

ผลคูณเชิงสเกลาร์ของเวกเตอร์ หรือภาษาอังกฤษคือ dot product  คือการนำเวกเตอร์มาดอทกันผลลัพธ์จากการนำเวกเตอร์มาดอทกันนี้จะเป็นสเกลาร์หรือว่าตัวเลข  เรามาดูนิยามของมันเลยครับ