เวกเตอร์ (vector)
ปริภูมิเวกเตอร์ (Vector space) ในการศึกษาระบบคณิตศาสตร์มาหลายระบบ เราจะพบว่ามีการด าเนินการบวก และ การคูณด้วยสเกลาร์ถา้ไม่คา นึงถึงลกัษณะของสมาชิกในระบบ แลว้เราจะพบว่าการดา เนินการเหล่าน้ีจะมีสมบตัิทางพีชคณิตที่เหมือนกนั ดงัน้นัการศึกษาทฤษฎีและ สมบตัิทวั่ ไป ของการดา เนินการดงักล่าวจะสามารถนำ ไปประยกุต์ ในคณิตศาสตร์ระบบต่างๆได้ซ่ึงระบบที่ดงักล่าวนี้เราจะเรียกว่า ปริภูมิเวกเตอร์ซึ่งในบทน้ีเราจะเริ่มจาก ระบบคณิตศาสตร์ที่เราคุ้นเคยมาก่อน แล้วจึงสรุปเป นบทนิยาม แล้วศึกษาตัวอย่างของปริภูมิเวกเตอร์ในลักษณะต่างๆต่อไป
การบวก
ถ้าต้องการรวม 2 เวกเตอร์นี้เข้าด้วยกัน นั่นคือหาผลลัพธ์ของ
+
เราสามารถทำได้ 2 วิธี ดังนี้
1. แบบหัวต่อหาง: เขียนเวกเตอร์
ก่อน จากนั้นเอาหางของ
มาต่อที่หัวของดังรูป
ผลลัพธ์ที่ได้คือเวกเตอร์ที่ลากจากหางของไปสิ้นสุดที่หัวของ
2. แบบหางต่อหาง: นำหางของทั้งสองเวกเตอร์มาต่อชนกันแล้วสร้างรูปสี่เหลี่ยมด้านขนาน(แสดงด้วยเส้นประสีเทา)ผลลัพธ์ที่ได้คือเวกเตอร์ที่ลากจากจุดหางที่ต่อกัน ไปจนถึงมุมทะแยงตรงข้ามของรูปสี่เหลี่ยมด้านขนานนั้น
จะเห็นได้ว่า เวกเตอร์ผลลัพธ์ที่ได้จากทั้งสองวิธีนี้เท่ากัน โดยมีขนาดและทิศทางดังแสดงตามลูกศรสีแดง
สำหรับการลบกันของเวกเตอร์ จริงๆ แล้วก็คือการบวกด้วยเวกเตอร์ที่เป็นลบ เช่น–=+(-) จากนั้นก็ดำเนินการต่อด้วยวิธีการที่กล่าวไปแล้วข้างต้น
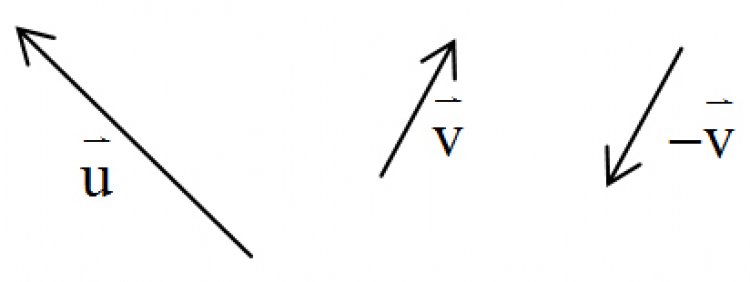
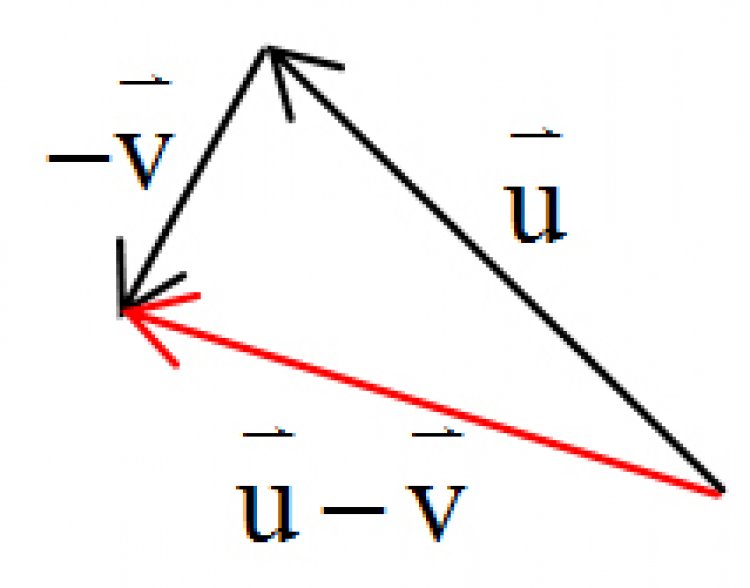
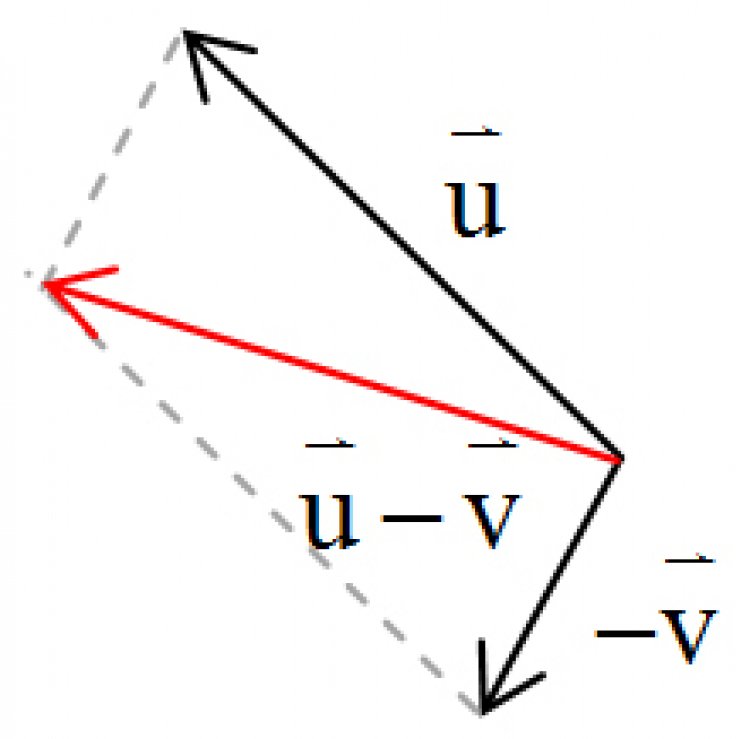
แปลงเวกเตอร์เป็น – ใช้วิธีหัวต่อหาง ใช้วิธีหางต่อหาง
2. เวกเตอร์ในระบบพิกัดฉาก 2 มิติ และ 3 มิติ
ลองดูรูปต่อไปนี้
