เอกลักษณ์และสมการตรีโกณมิติ

เอกลักษณ์ของฟังก์ชันตรีโกณมิติ เอกลักษณ์ของฟังก์ชันตรีโกณมิติ หมายถึง สมการตรีโกณมิติที่เป็นจริงเสมอ ไม่ว่าจะแทนที่ตัวแปลด้วยจำนวนจริงใดๆ ก็ตาม โดยการแทนที่ตัวแปลด้วยจำนวนจริงนั้นจะต้องทำให้แต่ละพจน์มีความหมายด้วย การพิสูจน์เอกลักษณ์ หมายถึง การพิสูจน์ให้เห็นจริงว่า กลุ่มพจน์ทางด้านซ้ายมือและขวามือ ของเครื่องหมายเท่ากับ เท่ากันเสมอ ในทุกๆ ค่าตัวแปร หลักการในการพิสูจน์เอกลักษณ์ 1. ควรพิสูจน์จากด้านที่ยุ่งยากไปหาด้านที่ง่ายกว่า 2. ควรจะเปลี่ยนฟังก์ชันตรีโกณมิติที่โจทย์กำหนดมาให้เป็นฟังก์ชัน sine หรือ cosine เพื่อที่จะทำให้การพิสูจน์เอกลักษณ์ง่ายขึ้น

เอกลักษณ์ตรีโกณมิติ คือการเท่ากันของฟังก์ชันตรีโกณมิติที่ต่างกัน และเป็นจริงสำหรับทุก ๆ ค่าของขนาดของมุม

เมื่อกำหนด A เป็นขนาดของมุมใดๆ ( 0 < A < 360) จะได้

sinA * cosA = 1

cosA * secA = 1

tanA * cotA = 1

cosA * tan A = sinA

sinA * cot A = cosA

sin² A * cos²A = 1

sec²A – tan²A = 1

cos²A – cot²A = 1

เมื่อกำหนด x และ y เป็นขนาดของมุมใดๆ ( 0 <  X,Y < 360 )จะได้

sin ( X + Y ) = sinX * cosY + cosX * sinY

sin ( X – Y ) = sinX * cosY – cosX * sinY

cos ( X + Y ) = cosX * cosY – sinX * sinY

cos ( X – Y ) = cosX * cosY + sinX * sinY

tan ( X + Y ) = tanX + tanY / 1 – tanX tanY

tan ( X – Y ) = tanX – tanY / 1 + tanX tanY

sinX + sinY = 2sin [ (X + Y) /2 ] cos [ ( X – Y ) / 2]

sinX – sinY = 2cos [ (X + Y) /2 ] sin [ ( X – Y ) / 2]

cosX + cosY = 2cos [ (X + Y) /2 ] cos [ ( X – Y ) / 2]

cosX – cosY = -2sin [ (X + Y) /2 ] sin [ ( X – Y ) / 2]

tanX + tanY = [ sin ( X + Y) ] / cosX cosY

tanX – tanY = [ sin ( X – Y) ] / cosX cosY

 

cotX + cotY = [ sin ( X + Y) ] / sinX sinY

cotX – cotY = [ -sin ( X – Y) ] / sinX sinY

เอกลักษณ์ตรีโกณมิติ คือการเท่ากันของฟังก์ชันตรีโกณมิติที่ต่างกัน และเป็นจริงสำหรับทุก ๆ ค่าของขนาดของมุม

 เมื่อกำหนด A เป็นขนาดของมุมใดๆ (0 ≤ A ≤ 2π) จะได้

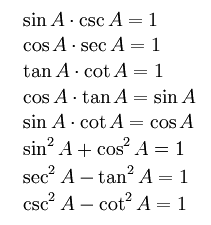
 เมื่อกำหนด x และ y เป็นขนาดของมุมใดๆ  (0 ≤ x ≤ 2π , 0 ≤ y ≤ 2π) จะได้

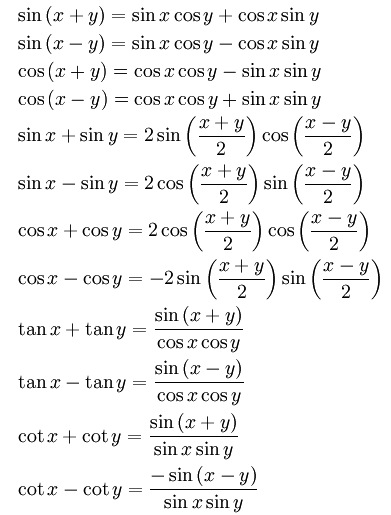
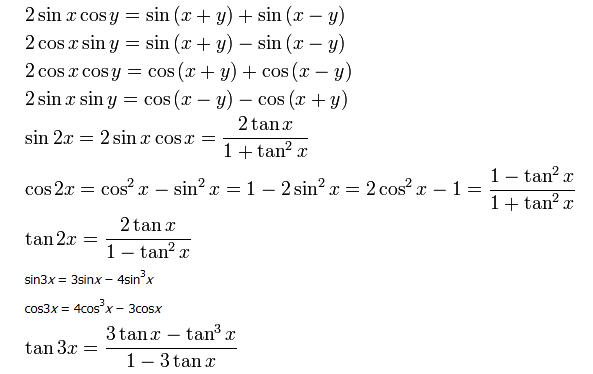
กฎของโคไซน์ และไซน์

 

กฎของโคไซน์ ในรูปสามเหลี่ยม ABC ใดๆ ถ้า a,b และ cเป็นความยาวของด้านตรงข้ามมุม A,B และ C ตามลำดับ จะได้    

a² = b² + c² – 2bc cosA

b² = c² + a² – 2ca cosB

c² = a² + b² – 2ab cosC

 

กฎของไซน์ ในรูปสามเหลี่ยม ABC ใดๆ ถ้า a,b และ c เป็นความยาวของด้านตรงข้ามมุม A,B และ C ตามลำดับ จะได้

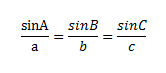
การหาระยะทางและความสูง  

ในการวัดระยะทางและความสูงของสิ่งใดก็ตาม บางครั้งจะใช้เครื่องมือสำหรับวัดมาใช้ในการวัดโดยตรงไม่ได้

เช่น การวัดสถานที่สองแห่งที่มีสิ่งกีดขวางกั้นตรงกลาง หรือการวัดความสูงของภูเขา เป็นต้น

เราสามารถนำความรู้ในเรื่องฟังก์ชันตรีโกณมิติ มาประยุกต์ใช้ในการคำนวณได้ อันได้แก่

– มุมก้ม (Angel of Depression) คือมุมที่วังลงไปจากแนวราบ (ระดับสายตา)

– และมุมเงย (Angle of Elevation)คือมุมที่วัดขึ้นจากแนวราบ

– รวมถึงการใช้กฎของไซน์และโคไซน์มาช่วยในการคำนวณ