แบบฝึกหัด ผลคูณคาร์ทีเซียน และคู่อันดับ ม.4 คณิตศาสตร์ ม.ปลาย

2. ผลคูณคาร์ทีเซียน(Cartesian  product)

ให้  A  และ B   เป็นเซตสองเซตใด ๆ  ผลคูณคาร์ทีเซียนของ  A  และ  B

เขียนแทนด้วย A×B (อ่านว่า A  ครอส B)  เป็นเซตของคู่อันดับทั้งหมดที่เป็นไปได้

โดยที่สมาชิกตัวแรกของคู่อันดับเป็นสมาชิกของ  A   และสมาชิกตัวหลังของคู่อับดับ

เป็นสมาชิกของ B

นั้นคือ  A×B = {(a , b) | a A , b  B }

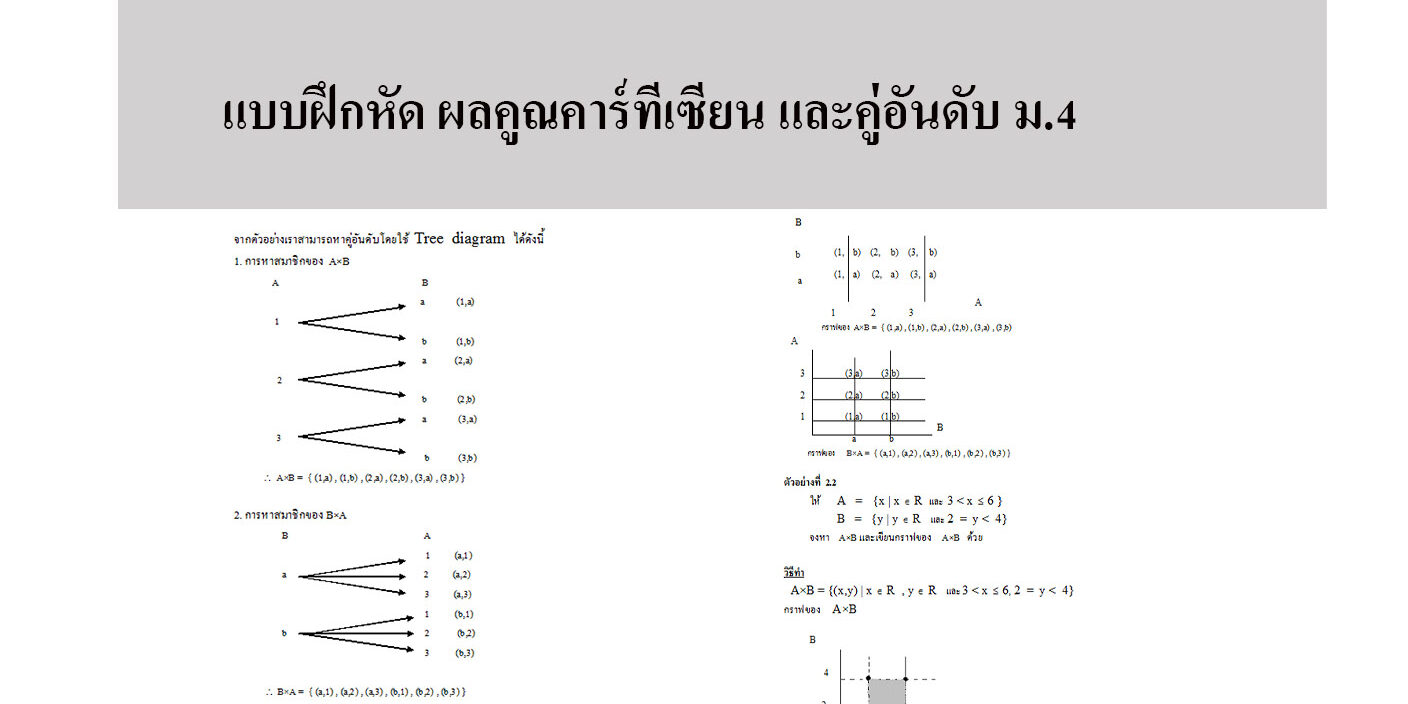
ตัวอย่างที่  2.1

การหาผลคูณคาร์ทีเซียน

กำหนด    A   =  {1,2,3}   ,       B =  {a,b}

1.  A×B =  { (1,a) , (1,b) , (2,a) , (2,b) , (3,a) , (3,b) }

2.  B×A =  { (a,1) , (a,2) , (a,3) , (b,1) , (b,2) , (b,3) }

3.  A×A = { (1,1) , (1,2) , (1,3) , (2,1) , (2,2) , (2,3) , (3,1) , (3,2) , (3,3) }

4.  B×B  = { (a,a) , (a,b) , (b,a) , (b,b) }

บทนิยาม    ผลคูณคาร์ทีเซียนของเซต  A  และ  B  คือเซตของคู่อันดับ (a,b) ทั้งหมด  โดยที่ a  เป็นสมาชิกของเซต  A  และ  b  เป็นสมาชิกของเซต  B

ผลคูณคาร์ทีเซียนของเซต  A  และ  B  เขียนแทนด้วย   A x B

เขียน   A x B   ในรูปเซตแบบบอกเงื่อนไขได้ดังนี้

A X B   =  {(a,b)| a A  และ  b  B}

ตัวอย่างที่ 3      A  =  {2,4,6}  ,  B  =  {a,b}

ดังนั้น     A x B  =  {(2,a),(2,b),(4,a),(4,b),(6,a),(6,b)}

n(AxB)   =  6

B x A   =  {(a,2),(a,4),(a,6),(b,2),(b,4),(b,6)}

n(AxB)   =  6

A x A   =  {(2,2),(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),(6,6)}

n(AxA)   =  9

ข้อสังเกต   1. ถ้า  A  มีจำนวนสมาชิก n ตัว ;  B  มีจำนวนสมาชิก  m  ตัว แล้ว  AxB    มีจำนวน สมาชิกทั้ง   หมดเท่ากับ  nm

2.  ถ้า  n(A) = n  ตัว  และ  n(B) = m  ตัว   ความสัมพันธ์จาก A ไป B ทั้งหมดเท่ากับ  2^nm