เอกภพสัมพัทธ์ (Relative Universe)คือ เซตที่ก าหนดให้ โดยมีข้อตกลงว่าจะไม่กล่าวถึงสิ่งใดนอกเหนือไปจากสมาชิกของเซตที่ก าหนดขึ้นนี้ ใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์แผนภาพของเวนน์ – ออยเลอร์(Venn-Euler Diagrams)
คือ แผนภาพที่เขียนเซตด้วยรูปปิดใด ๆ นิยมเขียนด้วยรูปสี่เหลี่ยมมุมฉาก แทนเอกภพสัมพัทธ์ U และเขียนเซตต่างๆ ซึ่งเป็นสับเซตของ U ด้วยรูปปิดอาจเป็น วงกลม วงรี หรือรูปปิดอื่น ๆ ลงในสี่เหลี่ยมผืนผ้า

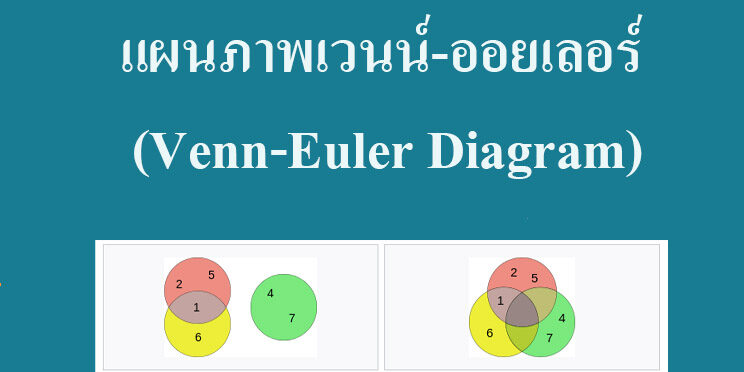
แผนภาพ “เวนน์-ออยเลอร์ (Venn-Euler Diagram)”

ในการสร้างอินโฟกราฟิกนั้น องค์ประกอบหนึ่งที่สำคัญที่ช่วยทำให้คนอ่านเข้าใจเนื้อหาได้เร็ว และง่ายขึ้น คือการใช้แผนภูมิ หรือภาพในการเล่าเรื่อง ซึ่งรูปแบบของแผนภูมิมีอยู่มากมายหลายประเภท  ไม่ว่าเป็น แผนภูมิแท่ง วงกลม แผนภูมิเส้น เป็นต้น แต่ในปัจจุบันก็มีแผนภูมิหรือแผนภาพที่หน้าตาแปลกใหม่ และถูกนำมาใช้ในการออกแบบมากขึ้น เชื่อว่าหลายคนต้องเคยเห็น เพียงแต่อาจจะยังไม่ค่อนเข้าใจถึงหลักการในการนำไปใช้ วันนี้จึงมาแนะนำแผนภาพที่เรียกว่า  “เวนน์-ออยเลอร์” (Venn-Euler Diagram)
แผนภาพเวนน์-ออยเลอร์ เป็นแผนภาพที่เราน่าจะคุ้นเคยเมื่อครั้งที่เรียนวิชาคณิตศาสตร์ ซึ่งแผนภาพประเภทนี้ใช้ในการอธิบายความสัมพันธ์ของข้อมูลที่มีการซ้อนทับ หรือไม่ซ้อนทับกัน โดยให้วงกลมแทนข้อมูลแต่ละชุด และใช้วิธีการจัดวางวงกลมที่แตกต่างกันในการแสดงความสัมพันธ์ของข้อมูล โดยในการจัดวางชุดข้อมูลสามารถแบ่งได้ดังนี้

ตัวอย่วง1 . ให้ U = I+
A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
C = {1, 2, 3, 4, 5, 6, 8}
ข้อใดคือแผนภาพที่แสดงความสัมพันธ์ของเซต A, B , C และ U ให้ลองวาดดูนะครับ

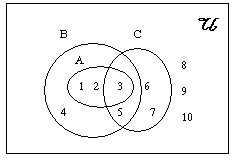
ตัวอย่วง2 .ถ้ากำหนดให้ U = {1,2,3,4,5,6,7,8,9,10} A = {1,2,3} , B = {1,2,3,4,5} , C = {3,5,6,7}

เราจะเขียนแผนภาพเวนน์–ออยเลอร์ แสดงเอกภพสัมพัทธ์ U และเซตย่อยต่าง ๆ ดังแผนภาพต่อไปนี้

การใช้แผนภาพเวนน์–ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล

เราจะวาดแผนภาพตามสมมติฐานที่เป็นไปได้ แล้วพิจารณาว่าแผนภาพแต่ละกรณีแสดงผลสรุปตามที่สรุปไว้หรือไม่ ถ้าทุกกรณีแสดงผลตามที่กหนด แสดงว่าสมเหตุสมผล ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปนั้นไม่สมเหตุสมผล โดยจะใช้การอ้างเหตุผลโดยตรรกบทของตรรกศาสตร์เข้ามาตรวจสอบ

ในการใช้แผนภาพเพื่อตรวจสอบความสมเหตุสมผล จะต้องวาดแผนภาพตามเหตุผลหรือสมมติฐานทุกกรณีที่เป็นไปได้ ถ้าทุกกรณีแสดงผลตามที่กำหนด จะได้ว่าข้อสรุปนั้น สมเหตุสมผล แต่ถ้ามีบางกรณีที่ไม่สอดคล้องกับผลสรุปแล้ว ผลสรุปนั้นจะไม่สมเหตุผมผล …

ตัวอย่างที่  .3     กำหนด   U   =   {x |  x  เป็นจำนวนนับที่น้อยกว่า  20}

A  =  {x |  x  เป็นจำนวนนับที่น้อยกว่า  10}

B  =  {x |  x  เป็นจำนวนคี่บวกที่น้อยกว่า  7}

จงเขียนแผนภาพเวนน์-ออยเลอร์

วิธีทำ       U   = {x |  x  เป็นจำนวนนับที่น้อยกว่า  20}

\    U   =   {1, 2, 3, . . . , 19}

A   =   {x |  x  เป็นจำนวนนับที่น้อยกว่า  10}

\    A   =   {1, 2, 3, . . . , 9}

B   =   {x |  x  เป็นจำนวนคี่บวกที่น้อยกว่า  7}

\    B   =   {1, 3, 5}

เขียนแผนภาพแทน  A และ  B  ได้ดังนี้