แรง มวล และกฏการเคลื่อนที่ สมดุลต่อการเคลื่อนที่
1.การหาแรงลัพธ์
2. การหาแรงลัพธ์ของ 2 แรง
3. การหาแรงลัพธ์ของ 3 แรง
4. การหาทิศของแรงที่กระทำต่อวัตถุจากลักษณะของการเคลื่อนที่
5. กฎการเคลื่อนที่ของนิวตัน
6. กฎการเคลื่อนที่ข้อที่ 1
7. กฎการเคลื่อนที่ข้อที่ 2
8. กฎการเคลื่อนที่ข้อที่ 3
9. แรงเสียดทาน
10. สมดุลของแรง
11. สมดุลต่อการเคลื่อนที่(translationalequilibrium)
12. สมดุลต่อการหมุน(rotational equilibrium)
การหาแรงลัพธ์โดยวิธีคำนวณ
แรง (Force) : F คือ สิ่งที่สามารถทำให้วัตถุเปลี่ยนสภาพการเคลื่อนที่ แรงจัดเป็นปริมาณเวกเตอร์ คือมีทั้งขนาด (ค่าที่เป็นตัวเลข) และทิศทาง มีหน่วยเป็น N (นิวตัน)
เมื่อมีแรงกระทำต่อวัตถุตั้งแต่สองแรงขึ้นไปน้อง ๆ จำเป็นต้องหาแรงลัพธ์แล้วนำค่าแรงลัพธ์นั้นไปใช้ในการหาคำตอบสุดท้ายของโจทย์ที่ซับซ้อนต่อไป
แรงที่กระทำต่อวัตถุสรุปได้หลักๆ อยู่ 4 แบบคือ
– แรงในทิศเดียวกัน
– แรงในทิศตรงข้าม
– แรงที่ตั้งฉากกัน
– แรงที่ทำมุมกัน (ที่ไม่ใช่มุมฉาก)
• วิธีที่ 1 ใช้การแตกแรงหรือแยกแรง •
การแตกแรงหรือแยกแรง คือการแยกแรง 1 แรงออกเป็นแรงองค์ประกอบ 2 แรงซึ่งตั้งฉากกันอยู่ตามแนวแกน x และแกน y
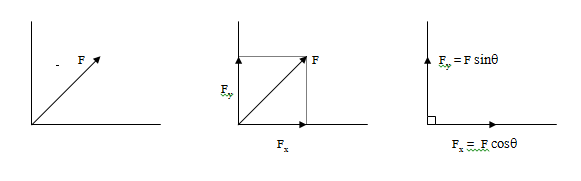
F เป็นขนาดของแรงที่มี F ทำมุม q กับแกนนอนหรือแกน x
Fx เป็นขนาดของแรงตามแนวแกน x
Fy เป็นขนาดของแรงตามแนวแกน y

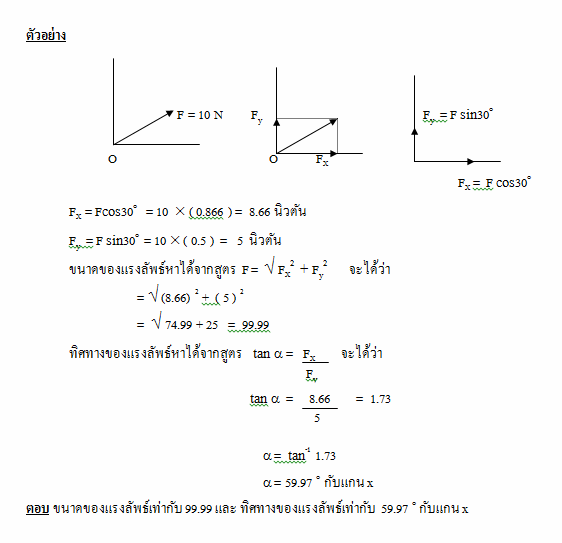
แรงลัพธ์
อำนาจอย่างหนึ่งที่ทำให้วัตถุหยุดนิ่งหรือเคลื่อนที่ได้ หรือกล่าวได้ว่าแรงสามารถทำให้วัตถุเปลี่ยนสภาพการเคลื่อนที่ แรงเป็นปริมาณเวคเตอร์ (ปริมาณที่ต้องบอกขนาดและทิศทาง)
หน่วยของแรง คือ นิวตัน < Newton สัญลักษณ์ N >
ถ้ามีแรงหลาย ๆ แรงมากระทำต่อวัตถุเดียวกัน ในเวลาเดียวกัน เสมือนกับว่า มีแรงเพียงแรงเดียวมากระทำต่อวัตถุนั้น เรียกแรงเสมือนแรงเดียวนี้ว่า แรงลัพธ์ (หรือกล่าวได้ว่าแรงลัพธ์คือผลรวมของแรงหลาย ๆแรงที่กระทำต่อวัตถุนั้น )
การหาแรงลัพธ์ เนื่องจากแรงเป็นปริมาณเวคเตอร์ดังนั้นการหาแรงลัพธ์คิดเหมือนกับ การหาเวคเตอร์ลัพธ์ โดยแทนแรงด้วยลูกศร ความยาวของลูกศรจะแทนขนาดของแรง และทิศของลูกศรจะแทนทิศทางของแรงที่กระทำ และวัตถุจะเคลื่อนที่ไปตามทิศของแรงลัพธ์
วิธีการหาแรงลัพธ์
1. การเขียนรูป (โดยแทนแรงด้วยลูกศร )
ใช้หางต่อหัว คือเอาหางของลูกศรที่แทนแรงที่ 2 มาต่อหัวลูกศรที่แทนแรงที่ 1
แล้วเอาหางลูกศรที่แทนแรงที่ 3 มาต่อหัวลูกศรที่แทนแรงที่ 2 …..ต่อกันไปจนหมด
โดยทิศของลูกศรที่แทนแรงเดิมไม่เปลี่ยนแปลง
ขนาดของแรงลัพธ์คือ ความยาวลูกศรที่ลากจากจุดเริ่มต้น ไปยังจุดสุดท้าย
มีทิศจากจุดเริ่มต้นไปจุดสุดท้าย
ตัวอย่าง เมื่อมีแรง A B และ C มากระทำต่อวัตถุ ดังรูป
2. โดยการคำนวณ
2.1. เมื่อแรงทำมุม 0 องศา (แรงไปทางเดียวกัน)
แรงลัพธ์ = ขนาดแรง ทั้งสองบวกกัน และทิศของแรงลัพธ์ มีทิศเดิม

แรงลัพธ์ = แรงมากลบด้วยแรงน้อย ทิศของแรงลัพธ์มีทิศเดียวกับแรงมาก

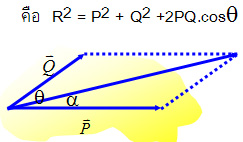
การหาแรงลัพธ์ของ 3 แรง
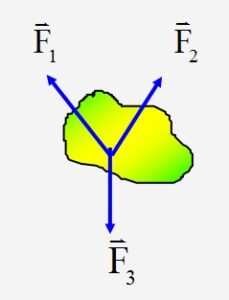
สมดุลของแรง 3 แรง
เมื่อมีแรง 3 กระทำต่อวัตถุ วัตถุจะสมดุลได้จะต้องอยู่ภายใต้เงื่อนไขคือ
1. แรงทั้งสามต้องอยู่ในระนาบเดียวกัน
2. แรงลัพธ์ = 0
3. แรงทั้งสามต้องพบกันที่จุดเดียวกันหรือแรงทั้งสามต้องขนานกัน
ทฤษฎีที่ใช้เกี่ยวกับการสมดุล
1. สมดุลของแรง 3 แรง
แรง 3 แรงจะสมดุลได้ มีเงื่อนไขดังนี้
1. แรงทั้งสามต้องอยู่ในระนาบเดียวกัน
2. แรงทั้งสามต้องพบกันที่จุดเดียวกัน หรือไม่ก็ต้องขนานกัน
3. แรงลัพธ์เท่ากับศูนย์
เรื่องแรงกับการเคลื่อนที่
แรง (force) เป็นสิ่งที่ทำให้วัตถุเปลี่ยนรูปร่าง เปลี่ยนทิศทาง เกิดการเคลื่อนที่หรือหรือหยุดนิ่งได้ แรงสามารถเปลี่ยนความเร็วของวัตถุได้ หรือกล่าวได้ว่าแรงทำให้วัตถุเกิดความเร่ง
ถ้ามีแรงขนาดเท่ากันกระทำต่อวัตถุในทิศทางตรงกันข้าม อาจจะทำให้เกิดการเปลี่ยนแปลงรูปร่างและขนาดของวัตถุ แต่ไม่มีการเคลื่อนที่ของวัตถุ
ลักษณะของแรง แรงเป็นปริมาณเวกเตอร์ มีทั้งขนาดและทิศทาง มีหน่วยเป็นนิวตัน (N) ใช้สัญลักษณ์ F เขียนแทนแรง การเขียนสัญลักษณ์ของแรงที่บอกทิศทางของแรงด้วยนั้น จะใช้ความยาวของเส้นตรงแทนขนาด และใช้หัวลูกศรแทนทิศทางของแรง เรียกว่า เวกเตอร์ของแรง
ใบความรู้ เรื่อง แรงแบบต่างๆ
แรงเคลื่อนที่และตำแหน่งของวัตถุ
การเคลื่อนที่ของวัตถุมีการเคลื่อนที่แบบต่างๆ เช่น การเคลื่อนที่ในแนวตรง แนวโค้ง และการเคลื่อนที่เป็นวงกลม ซึ่งในการเคลื่อนที่นั้นระบุว่า วัตถุอยู่ที่ใดต้องกำหนดจุดอ้างอิง ระยะทางและทิศที่วัตถุนั้นห่างจากจุดอ้างอิง ซึ่งเรียกว่า การกระจัด ซึ่งการกระจัดเป็นปริมาณเวกเตอร์ โดยปริมาณเวกเตอร์เป็นปริมาณที่มีทั้งขนาดและทิศทาง เขียนแทนด้วยลูกศร ความยาวของลูกศรแทนขนาด และหัวลูกศรแทนทิศทาง วัตถุที่กำลังเคลื่อนที่จะเคลื่อนที่เร็วหรือช้า พิจารณาจากระยะทางที่ได้หรือการกระจัดที่ได้เทียบกับเวลาที่ใช้ในการเคลื่อนที่
การเคลื่อนที่แบบต่างๆ มีลักษณะเฉพาะของการเคลื่อนที่
· การเคลื่อนที่แนวเส้นตรง : วัตถุจะเคลื่อนที่ในแนวเดิม (ทิศเดิมหรือทิศตรงข้าม) โดยอาจมีแรงกระทำต่อวัตถุหรือไม่ก็ได้ ถ้ามีแรงกระทำ ทิศของแรงที่กระทำจะอยู่ในแนวเดียวกับแนวการเคลื่อนที่ของวัตถุเสมอ
· การเคลื่อนที่แนวโค้ง : วัตถุจะมีการเคลื่อนที่ 2 แนวพร้อมๆ กัน เช่น เคลื่อนที่ในแนวราบและในแนวดิ่ง แรงที่กระทำต่อวัตถุจีทิศคงตัวตลอดเวลา โดยทำมุมใดๆ กับทิศของความเร็ว เช่น แรงดึงดูดของโลก
· การเคลื่อนที่วงกลม : วัตถุเคลื่อนที่เป็นส่วนโค้งรอบจุดๆ หนึ่ง โดยมีแรงกระทำในทิศเข้าสู่ศูนย์กลาง
· การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย : วัตถุจะเคลื่อนที่กลับไปมาซ้ำรอยเดิมโดยมีแอมพลิจูดคงตัว
แรงกับการเคลื่อนที่ของวัตถุ (แรงที่กระทำต่อวัตถุ)
การออกแรงกระทำต่อวัตถุอาจทำให้วัตถุเคลื่อนที่ได้ หรือวัตถุอาจไม่เคลื่อนที่ เนื่องจากมีแรงย่อยอื่นมาร่วมกระทำ ทำให้เกิดการหักล้างของแรงในปริมาณเวกเตอร์ ดังนั้นวัตถุที่จะเคลื่อนที่ได้หรือไม่ได้ก็ขึ้นอยู่กับแรงลัพธ์ที่มากระทำต่อวัตถุนั่นเอง
เมื่อออกแรงกระทำต่อวัตถุแล้ววัตถุไม่เคลื่อนที่ เนื่องจากถูกหักล้างด้วยแรงอื่นที่ร่วมกระทำต่อวัตถุนั้น แต่ไม่ว่าวัตถุนั้นจะเคลื่อนที่หรือไม่เคลื่อนที่ก็ตามจะเกิดแรงลัพธ์ของวัตถุเสมอ
แรงเป็นปริมาณที่มีขนาดและทิศทาง แรงจึงเป็นปริมาณเวกเตอร์ การรวมแรงต้องรวมแบบเวกเตอร์ ในการรวมแรงหลายๆ แรงที่กระทำต่อวัตถุ ถ้าผลรวมของแรงที่ได้เป็นศูนย์แสดงว่า วัตถุนั้นอยู่ในสภาพสมดุล เมื่อปล่อยวัตถุ วัตถุนั้นจะตกลงสู่พื้นดิน แสดงว่ามีแรงกระทำต่อวัตถุ ซึ่งแรงนั้นเกิดจากแรงดึงดูดที่โลกกระทำต่อวัตถุ หรือที่เรียกว่า แรงโน้มถ่วงของโลก หรือน้ำหนักของวัตถุนั่นเอง แรงโน้มถ่วงนี้จะมีค่ามากหรือน้อยขึ้นอยู่กับมวลของวัตถุ ในการลากวัตถุให้เคลื่อนที่ไปบนพื้นผิวจะมีแรงต้านการเคลื่อนที่ เรียกแรงนี้ว่า แรงเสียดทาน ซึ่งแรงเสียดทานจะมีค่ามากหรือน้อยขึ้นอยู่กับลักษณะผิวสัมผัสระหว่างวัตถุทั้งสองและแรงที่วัตถุกดพื้น กิจกรรมบางอย่างต้องการให้ผิวสัมผัสมีแรงเสียดทาน แต่กิจกรรมบางอย่างต้องการลดแรงเสียดทานระหว่างผิวสัมผัส
เมื่อออกแรงแล้วทำให้วัตถุเคลื่อนที่ไปตามแนวแรงนั้น เรียกว่า มีการทำงาน คำนวณหาค่าของงานที่ทำได้จากผลคูณของแรงและระยะทางในแนวเดียวกันกับแรง และกำหนดให้งานที่ทำได้ในหนึ่งหน่วยเวลา คือ กำลัง
ในบางกรณี เมื่อออกแรงกระทำต่อวัตถุอาจทำให้วัตถุหมุน เรียกว่าเกิดโมเมนต์ของแรง ซึ่งเกิดเมื่อแรงที่กระทำมีทิศตั้งฉากกับระยะทางจากจุดหมุนไปยังแนวแรง การหมุนนี้มีทั้งหมุนในทิศตามเข็มนาฬิกา และทวนเข็มนาฬิกา โดยถ้าผลรวมของโมเมนต์ตามเข็มนาฬิกาเท่ากับผลรวมของโมเมนต์ทวนเข็มนาฬิกา วัตถุจะอยู่ในสภาพสมดุล
เมื่อมีแรงกระทำต่อวัตถุทำให้วัตถุเคลื่อนที่สามารถวัดอัตราเร็วหรือขนาดของความเร็วของการเคลื่อนที่ได้จากการใช้เครื่องเคาะสัญญาณเวลา วัตถุที่เคลื่อนที่โดยมีความเร็วเปลี่ยนไป เรียกว่า วัตถุเคลื่อนที่โดยมีความเร่ง โดยความเร่งจะมีทิศเดียวกับทิศของแรงลัพธ์ที่กระทำต่อวัตถุ
การเคลื่อนที่ของวัตถุนอกจากจะเคลื่อนที่ในแนวตรงแล้ว ยังมีการเคลื่อนที่แบบอื่นอีก เช่น การเคลื่อนที่แบบโพรเจคไทล์ ซึ่งเป็นการเคลื่อนที่แนวโค้ง โดยได้ระยะทางในแนวราบและแนวดิ่งพร้อมๆ กัน การเคลื่อนที่ในแนววงกลม เป็นการเคลื่อนที่ที่มีแรงกระทำต่อวัตถุในทิศเข้าสู่ศูนย์กลาง
นิวตันอธิบายการเคลื่อนที่ของดาวเคราะห์ ตามกฎของเคปเลอร์
การค้นพบกฎทั้งสามข้อนี้ นำไปสู่การค้นพบ “กฎความโน้มถ่วงแห่งเอกภพ” (The Law of Universal) “วัตถุสองชิ้นดึงดูดกันด้วยแรงซึ่งแปรผันตามมวลของวัตถุ แต่แปรผกผันกับระยะทางระหว่างวัตถุยกกำลังสอง” ซึ่งเขียนเป็นสูตรได้ว่า
| F = G (m1m2/r2) โดยที่ F = แรงดึงดูดระหว่างวัตถุ
m1 = มวลของวัตถุชิ้นที่ 1 m2 = มวลของวัตถุชิ้นที่ 2 r = ระยะห่างระหว่างวัตถุทั้ง 2 ชิ้น G = ค่าคงที่ของแรงโน้มถ่วง = 6.67 x 10-11 newton m2/kg2 |
บางครั้งเราเรียกกฎข้อนี้อย่างง่ายๆ ว่า “กฎการแปรผกผันยกกำลังสอง” (Inverse square law) นิวตันพบว่า “ขนาดของแรง จะแปรผกผันกับ ค่ากำลังสองของระยะห่างระหว่างวัตถุ”
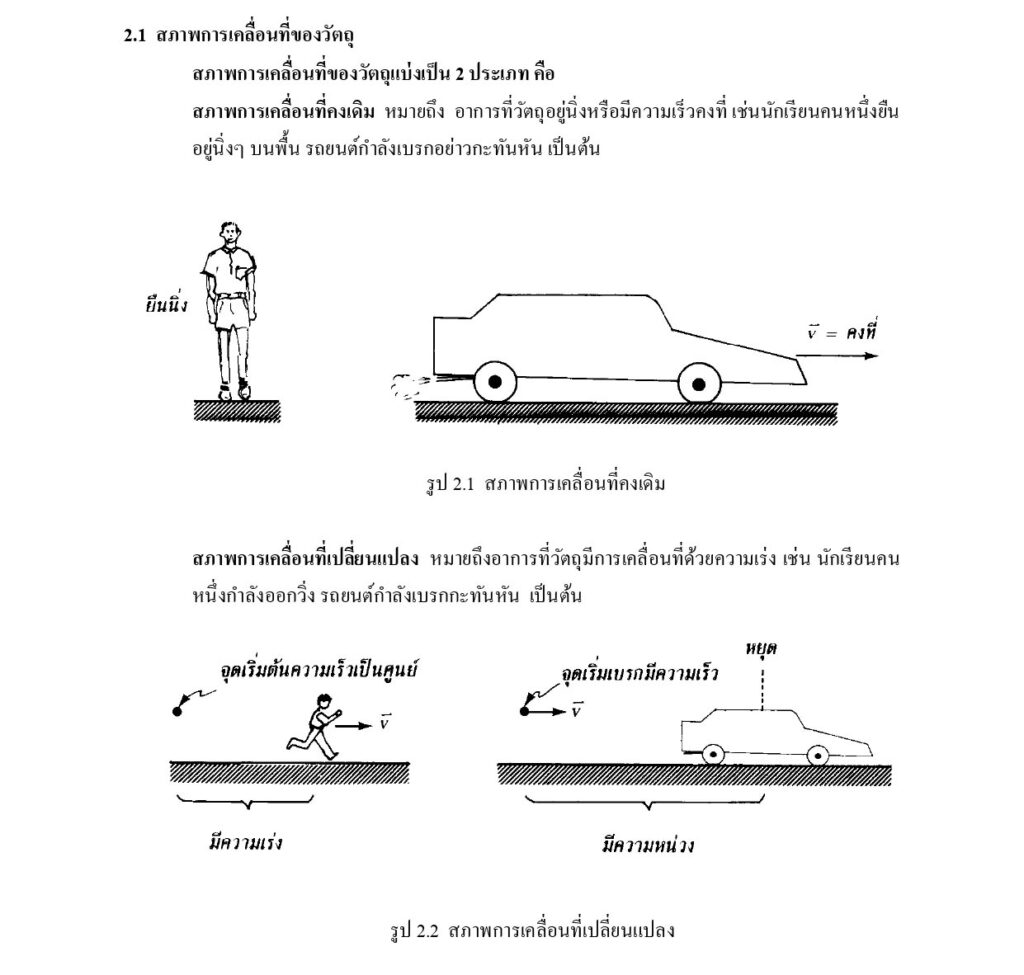
ตัวอย่าง: เมื่อระยะทางระหว่างวัตถุเพิ่มขึ้น 2 เท่า แรงดึงดูดระหว่างวัตถุจะลดลง 4 เท่า ดังที่แสดงในภาพที่ 6 เขาอธิบายว่า การร่วงหล่นของผลแอปเปิล ก็เช่นเดียวกับการร่วงหล่นของดวงจันทร์ ณ ตำแหน่งบนพื้นผิวโลก สมมติว่าแรงโน้มถ่วงบนพื้นผิวโลกมีค่า = 1 ระยะทางจากโลกถึงดวงจันทร์มีค่า 60 เท่าของรัศมีโลก ดังนั้นแรงโน้มถ่วง ณ ตำแหน่งวงโคจรของดวงจันทร์ย่อมมีค่าลดลง = 602 = 3,600 เท่า
ภาพที่ 7 การเคลื่อนที่ในอวกาศ
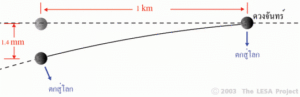
ในภาพที่ 8 แสดงให้เห็นว่า ใน 1 วินาที ดวงจันทร์เคลื่อนที่ไปได้ 1 กิโลเมตร จะถูกโลกดึงดูดให้ตกลงมา 1.4 มิลลิเมตร เมื่อดวงจันทร์โคจรไปได้ 1 เดือน ทั้งแรงตั้งต้นของดวงจันทร์ และแรงโน้มถ่วงของโลก ก็จะทำให้ดวงจันทร์โคจรได้ 1 รอบพอดี เราเรียกการตกเช่นนี้ว่า “การตกแบบอิสระ” (Free fall) อันเป็นหลักการซึ่งมนุษย์นำไปประยุกต์ใช้กับการส่งยานอวกาศ และดาวเทียม ในยุคต่อมา
ภาพที่ 8 การเคลื่อนที่ของดวงจันทร์
ตอนที่เคปเลอร์ค้นพบกฎการเคลื่อนที่ของดาวเคราะห์ ซึ่งได้จากผลของการสังเกตการณ์ในคริสต์ศตวรรษที่ 16 นั้น เขาไม่สามารถอธิบายว่าเหตุใดจึงเป็นเช่นนั้น จวบจนอีกหนึ่งศตวรรษต่อมา นิวตันได้ใช้กฎการแปรผกผันยกกำลังสอง อธิบายเรื่องการเคลื่อนที่ของดาวเคราะห์ ตามกฎทั้งสามข้อของเคปเลอร์ ดังนี้
• ดาวเคราะห์โคจรรอบดวงอาทิตย์เป็นรูปวงรี เกี่ยวเนื่องจากระยะทางและแรงโน้มถ่วงจากดวงอาทิตย์
• ในวงโคจรรูปวงรี ดาวเคราะห์จะเคลื่อนที่เร็ว ณ ตำแหน่งใกล้ดวงอาทิตย์ และเคลื่อนที่ช้า ณ ตำแหน่งไกลจากดวงอาทิตย์ เนื่องจากอิทธิพลของระยะห่างระหว่างดวงอาทิตย์
• ดาวเคราะห์ดวงในเคลื่อนที่ได้เร็วกว่าดาวเคราะห์ดวงนอก เป็นเพราะว่าอยู่ใกล้กับดวงอาทิตย์มากกว่า จึงมีแรงโน้มถ่วงระหว่างกันมากกว่า
ความเร็ว (Speed) หมายถึง ระยะทางที่วัตถุเคลื่อนที่ไปใน 1 หน่วยของเวลา (ระยะทาง/เวลา)
ความเร่ง (Acceleration) หมายถึง ความเร็วของวัตถุที่เปลี่ยนแปลงไปใน 1 หน่วยเวลา (ระยะทาง/เวลา)/เวลา
ตัวอย่าง:
ในวินาทีแรก รถเคลื่อนที่ด้วยความเร็ว 1 เมตร/วินาที ในวินาทีที่สอง รถคันนี้เคลื่อนที่ด้วยความเร็ว 5 เมตร/วินาทีเพราะฉะนั้น รถคันนี้มีความเร่ง 4 (เมตร/วินาที)/วินาที






