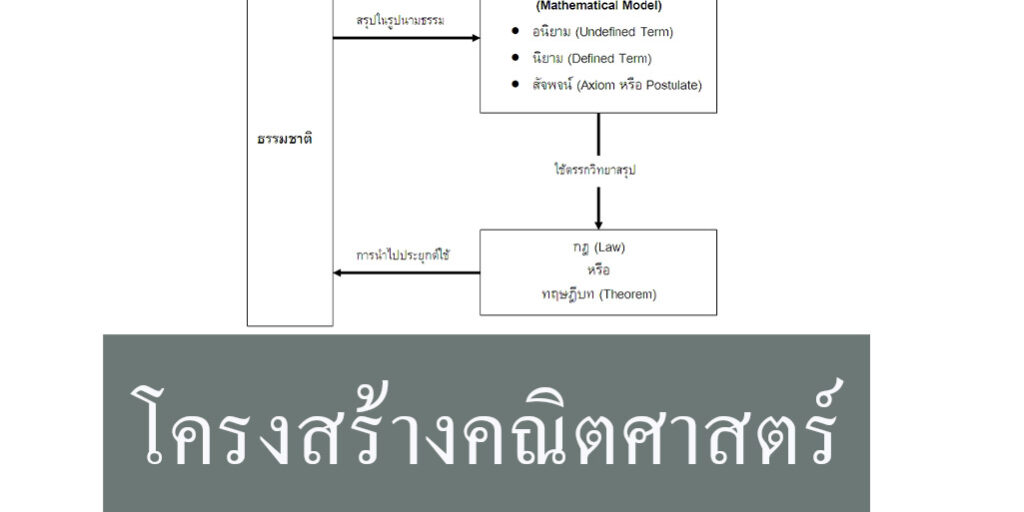
โครงสร้างของระบบคณิตศาสตร์

พจนานุกรมฉบับราชบัณฑิตยสถาน พ.ศ.2525 หน้า 162 ได้ให้ความหมายของคณิตศาสตร์ไว้ ดังนี้ “คณิตศาสตร์เป็นวิชาที่ว่าด้วยการคำนวณ”  จะเห็นได้ว่าทุกประเทศต่างตระหนักถึงคุณค่าและความสำคัญของคณิตศาสตร์ จึงกำหนดให้ทุกคนต้องเรียนคณิตศาสตร์ คณิตศาสตร์มีลักษณะเป็นภาษาสากล จากการที่คณิตศาสตร์มีลักษณะเฉพาะที่สำคัญและมีคุณค่า  ที่ว่า “มีความเป็นสากล” นี้ คณิตศาสตร์จึงเป็นศาสตร์ที่นักวิทยาศาสตร์และนักเทคโนโลยีในโลกต่างใช้เป็นเครื่องมือในการสื่อสารหรือสื่อความหมายซึ่งกันและกัน ทั้งนี้เพื่อเรียนรู้และถ่ายทอดความรู้ทางด้านวิทยา-ศาสตร์และเทคโนโลยีให้แก่กันและกัน Gauss (ค.ศ.1777 – 1855) หนึ่งในสามนักคณิตศาสตร์ที่ยิ่งใหญ่ที่สุดตลอดกาลได้กล่าวยกย่องให้คณิตศาสตร์เป็นราชินีของวิทยาศาสตร์  (Mathematics is the Queen of the Science)

ธรรมชาติและลักษณะเฉพาะของคณิตศาสตร์ที่สำคัญประการหนึ่งคือ “คณิตศาสตร์มีลักษณะเป็นวิทยาศาสตร์” เพราะคณิตศาสตร์สามารถอธิบายได้และทุกคนยอมรับ

นอกจากความเป็นภาษาสากลและความเป็นวิทยาศาสตร์ที่คณิตศาสตร์มีอยู่ในตัวแล้ว คณิตศาสตร์ยังมีลักษณะเป็นตรรกวิทยา เพราะคณิตศาสตร์เป็นศาสตร์ที่ว่าด้วยเหตุผล คณิตศาสตร์เป็นศาสตร์ที่ใช้ศึกษาระบบที่สร้างขึ้นโดยอาศัยข้อตกลงและใช้เหตุผลตามลำดับ

ในการศึกษาวิชาคณิตศาสตร์ ไม่ว่าจะสาขาใดก็ตาม จะพบว่าในตอนเริ่มต้นของการศึกษาจะต้องเรียนรู้ถึงคำใหม่ๆ ในสาขานั้นๆ คำใหม่เหล่านี้บางคำก็จำเป็นต้องให้ความหมายที่ชัดเจน โดยกำหนดคำนิยาม (Define Term) ของคำนั้นๆ แต่บางคำก็ไม่จำเป็นต้องให้นิยาม เพราะให้นำยามไปก็ไม่มีประโยชน์ เช่น คำว่า จุด เส้น เซต เป็นต้น ซึ่งเราพูดถึงคำที่ไม่ให้นิยามเหล่านี้ว่า คำอนิยาม (Undefine Term)

นอกจากคำว่านิยาม และคำอนิยามแล้ว เราจะพบสิ่งที่มีความสำคัญอีกประการหนึ่ง คือ ข้อความที่ยอมรับหรือมีข้อตกลงว่าเป็นความจริงโดยมไม่ต้องมีการพิสูจน์ ซึ่งข้อตกลงเหล่านี้เรียกว่า สัจพจน์ (Postulate หรือ Axiom) ซึ่งสัจพจน์นี้มีความสำคัญกับคณิตศาสตร์มาก เพราะนักคณิตศาสตร์ตั้งแต่อดีตเชื่อว่าก่อนที่เราจะพิสูจน์ข้อความใดข้อความหนึ่งว่าถูกต้องนั้น เราต้องยอมรับสิ่งใดสิ่งหนึ่งว่าถูกต้องก่อน ไม่เช่นนั้นเราก็ไม่สามารถพิสูจน์ข้อความนั้นได้

จากนิยาม อนิยาม และสัจพจน์ เราสามารถพิสูจน์ข้อความใหม่ๆ ได้อีกมากมาย ข้อความที่พิสูจน์ได้เหล่านี้เรียกว่า ทฤษฎีบท (Theorem) และตรรกศาสตร์จะมีความสำคัญมากในช่วงนี้ กล่าวคือ ตรรกศาสตร์จะกลายเป็นเครื่องมือในการพิสูจน์ทฤษฎีบทนั่นเอง จะเห็นว่าตรรกศาสตร์นั้นมีความสำคัญมากเพียงใดในวิชาคณิตศาสตร์

ในทางคณิตศาสตร์ เราเรียกระบบที่ประกอบด้วยบทนิยาม คำอนิยาม สัจพจน์ และทฤษฎีบท ว่าเป็นโครงสร้างของระบบคณิตศาสตร์ (Mathematical System Structure)

โครงสร้างของคณิตศาสตร์ซึ่งอยู่ในรูปที่สมบูรณ์แล้ว จะเริ่มต้นด้วยธรรมชาติ ซึ่งอาจจะเป็นเนื้อหาสาระทางฟิสิกส์ ชีววิทยา เศรษฐศาสตร์ จิตวิทยา สังคมศาสตร์ ธุรกิจ ยุทธศาสตร์ ฯลฯ ซึ่งหากว่าเราพิจารณาเนื้อหาเหล่านี้แล้วสรุปให้อยู่ในรูปนามธรรม เพื่อสร้างแบบจำลองทางคณิตศาสตร์ของเนื้อหานั้นๆ เราจะต้องอาศัยอนิยาม  นิยาม ตลอดจนสัจพจน์ มาใช้สรุปตามหลักตรรกวิทยาเพื่อให้ได้เป็นกฎ หรือทฤษฎีบท จากนั้นมนุษย์จะได้นำกฎหรือทฤษฎีบทไปประยุกต์ใช้ให้เกิดประโยชน์แก่ธรรมชาติต่อไป

โครงสร้างคณิตศาสตร์

คณิตศาสตร์ประกอบด้วยส่วนประกอบที่สำคัญ 4 ส่วน คือ อนิยาม นิยาม สัจพจน์ และทฤษฎีบท

            

            1. อนิยาม (Undefined Terms) หมายถึง คำหรือข้อความที่มีการตกลงกันว่าไม่ ต้องให้ความหมาย หรือคำจำกัดความ แต่เข้าใจตรงกันเป็นสากล

     ตัวอย่าง เช่น จุด เส้นตรง ระนาบ เซต สมาชิก เป็นสมาชิก

            2. บทนิยาม (Defined Terms) หมายถึง คำหรือข้อความที่มีการให้ความหมาย

หรือคำจำกัดความไว้อย่างชัดเจน เพื่อทุกคนจะได้มีความเข้าใจที่ตรงกัน

ตัวอย่าง เช่น “รูปสามเหลี่ยม” คือ รูปที่ประกอบด้วยจุด ๓ จุด และเส้นตรง ๓ เส้น และแต่ละเส้นมีจุดที่ปลาย ๒ จุด และทั้ง ๓ จุดไม่อยู่ในแนวเส้นตรงเดียวกัน

     

            หลักเกณฑ์ในการสร้างบทนิยาม

1.บทนิยามที่ดีต้องระบุสมบัติที่เด่นชัดลงไปให้เห็น เพื่อที่จะทำความเข้าใจได้ง่ายและชัดเจน

2. บทนิยามที่ดีต้องสั้น กะทัดรัด และประหยัดคำ

3. บทนิยามของคำคำหนึ่งจะต้องมีเพียงแบบเดียวเท่านั้น

4. บทนิยามที่ดีจะต้องย้อนกลับได้

5. บทนิยามที่ดีต้องประกอบด้วยคำอนิยามหรือคำนิยามที่มีมา

6. บทนิยามที่ดีจะต้องไม่มีข้อโต้แย้ง

7. บทนิยามที่ดีเมื่อกำหนดขึ้นมาในระบบหนึ่งแล้วจะต้องบอกได้ว่ามีอะไรเป็นหรือไม่เป็นตามบทนิยามนั้น

            3. สัจพจน์ (Axiom / postulate) หมายถึง ข้อความที่ตกลงกันและยอมรับว่าเป็นความจริงโดยไม่ต้องพิสูจน์ และนำไปอ้างเพื่อการพิสูจน์ข้อความอื่นว่าเป็นความจริงได้

สัจพจน์แยกได้เป็น ๓ แบบ คือ

– สมมติฐาน/ข้อสมมติ

– สิ่งที่เห็นจริงแล้ว

– ข้อตกลงหรือกติกา

            4. ทฤษฎีบท (Theorem) หมายถึง ข้อความที่ยอมรับว่าเป็นความจริงโดยที่ข้อความเหล่านี้ได้มีการพิสูจน์โดยอาศัยจากทฤษฎีบท นิยาม สัจพจน์ และวิธีการอย่างมีเหตุผล และข้อพิสูจน์นั้นเป็นการอ้างเหตุผลที่สมเหตุสมผล

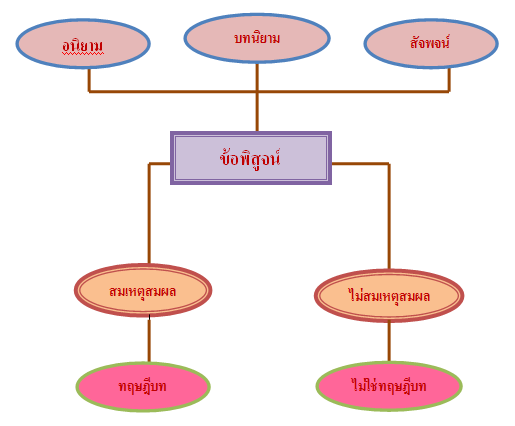
มนุษย์รู้จักการให้เหตุผล เพื่อเป็นการสนับสนุนความเชื่อหรือเพื่อหาความจริงหรือข้อสรุปในเรื่องใดเรื่องหนึ่งมาตั้งแต่ครั้งโบราณ การให้เหตุผลทางคณิตศาสตร์ที่สำคัญมีอยู่ 2 วิธี คือ

1. การให้เหตุผลแบบนิรนัย (Deductive Reasoning)

2. การให้เหตุผลแบบอุปนัย (Inductive Reasoning)

กระบวนการให้เหตุผล เป็นกระบวนการซึ่งนำเอาข้อความหรือปรากฏการณ์ต่างๆที่เป็นเหตุ (ข้อกำหนด) อาจจะหลายอันมาวิเคราะห์และแจกแจงแสดงความสัมพันธ์หรือความต่อเนื่องเพื่อทำให้เกิดข้อความใหม่หรือปรากฏการณ์ใหม่ๆขึ้น ซึ่งเรียกว่า ผล/ข้อยุติ (Conclusion)