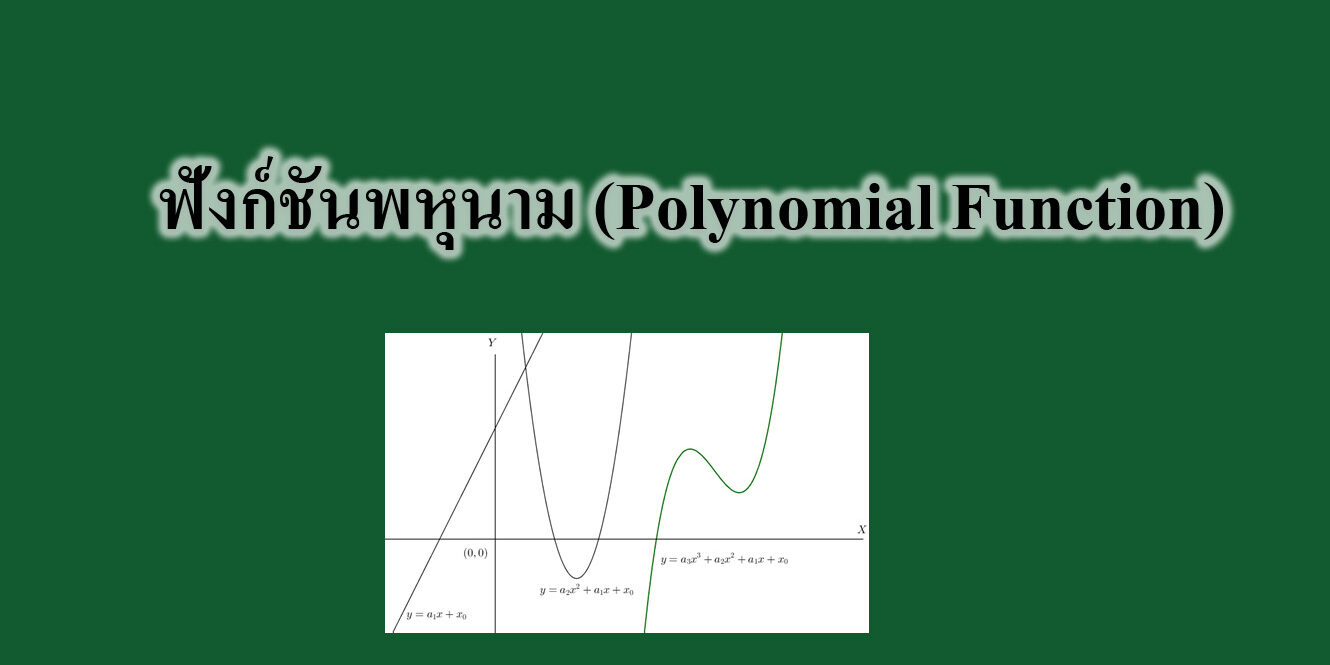
ฟังก์ชันพหุนาม (Polynomial Function)
สมการพหุนามที่มีสัมประสิทธิ์เป็นจำนวนจริง อาจไม่มีคำตอบที่เป็นจำนวนจริง เช่น สมการ x2 + 1 = 0 , x2 + x 1 = 0 ทฤษฎีบทต่อไปนี้ยืนยันว่าสมการพหุนามจะมีคำตอบเป็นจำนวนเชิงซ้อนเสมอ
ทฤษฎีบทหลักมูลของพืชคณิต (Fundamental Theorem of Algebra)
ถ้า p(x) เป็นพหุนามที่มีดีกรีมากกว่าศูนย์แล้ว สมการ p(x) = 0
จะมีคำตอบที่เป็นจำนวนเชิงซ้อนอย่างน้อยหนึ่งคำตอบ
การพิสูจน์ทฤษฎีบทหลักมูลของพีชคณิตต้องอาศัยความรู้ระดับสูง จึงจะขอไม่กล่าวถึงในที่นี้ อย่างไรก็ตามผลที่ตามมาของทฤษฎีบทหลักมูลพีชคณิต
ฟังก์ชันพหุนาม Polynomial Function
พหุนาม คือนิพจน์ที่สร้างจากตัวแปรอย่างน้อยหนึ่งตัวและค่าคงที่ โดยใช้การดำเนินการแค่ การบวก การลบ และการคูณ
ตัวอย่างเช่น นิพจน์ y(2xz3 − 4)x − 2 + (0.9x + z)y เป็นพหุนาม (เนื่องจาก z3 เป็นการเขียนย่อจาก z\cdot z\cdot z) แต่นิพจน์ {1 \over x^2 + 1} ไม่ใช่พหุนาม เนื่องจากมีการหาร เช่นเดียวกับ นิพจน์ (5 + y)x เนื่องจากไม่สามารถเขียนให้อยู่ในรูปของการคูณกันที่ไม่ขึ้นกับค่าของตัวแปร x ได้ นอกจากนี้ ยังมีการนิยาม พหุนาม ในรูปแบบจำกัด กล่าวคือ พหุนามคือ นิพจน์ที่เป็นผลรวมของผลคูณระหว่างตัวแปรกับค่าคงที่ ยกตัวอย่างเช่น 2x2yz3 − 3.1xy + yz − 2 อย่างไรก็ตาม ข้อจำกัดนี้เป็นเพียงข้อจำกัดที่ผิวเผิน เนื่องจากสามารถใช้กฎการ แจกแจงแปลง พหุนามภายใต้นิยามแรกให้เป็นพหุนามภายใต้นิยามที่สองได้ ในการใช้งานทั่วไปมักไม่แยกแยะความแตกต่างทั้งสอง นอกจากนี้ในบริบททั่วไปมักนิยมถือว่าโดยทั่วไปพหุ นามจะอยู่ในรูปแบบจำกัดนี้ แต่เมื่อต้องการแสดงว่าอะไรเป็นพหุนาม มักใช้รูปแบบแรกเนื่องจากสะดวกมากกว่า
ฟังก์ชันพหุนาม คือ ฟังก์ชันที่นิยามด้วยพหุนาม ตัวอย่างเช่น ฟังก์ชัน f นิยามด้วย f(x) = x3−x เป็นฟังก์ชันพหุนาม ฟังก์ชันพหุนามเป็นฟังก์ชันเรียบประเภท หนึ่งที่สำคัญ โดยคำว่า
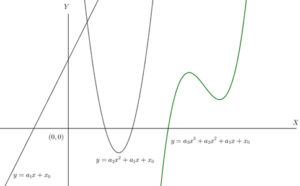
ตรีโกณมิติ (Trigonometry) เรียกอีกอย่างหนึ่งว่า Circular Function คือ ฟังก์ชันของมุม ซึ่งมีความสำคัญในการศึกษารูปสามเหลี่ยมและปรากฏการณ์ในลักษณะเป็นคาบ ฟังก์ชันอาจนิยามด้วยอัตราส่วนของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก หรืออัตราส่วนของพิกัดของจุดบนวงกลมหนึ่งหน่วย หรือนิยามในรูปทั่วไปเช่น อนุกรมอนันต์ หรือสมการเชิงอนุพันธ์ รูปสามเหลี่ยมที่นำมาใช้จะอยู่ในระนาบแบบยุคลิดดังนั้น ผลรวมของมุมทุกมุมจึงเท่ากับ 180° เสมอ
ฟังก์ชันตรีโกณมิติพื้นฐานทั้งหมดในปัจจุบัน มีฟังก์ชันตรีโกณมิติอยู่ 6 ฟังก์ชันที่นิยมใช้กัน ดังนี้
| ฟังก์ชัน | ตัวย่อ |
| ไซน์ (Sine) | sin |
| โคไซน์ (Cosine) | tan (หรือ tg) |
| แทนเจนต์ (Tangent) | cot (หรือ ctg หรือ ctn) |
| โคแทนเจนต์ (Cotangent) | sec |
| ซีแคนต์ (Secant) | csc (หรือ cosec) |
ฟังก์ชันค่าสัมบูรณ์
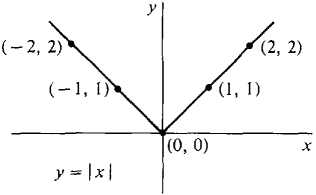
ฟังก์ชันค่าสัมบูรณ์ (Absolute Value Function)
ฟังก์ชันค่าสมบูรณ์ถูกกำหนดโดยกฎซึ่งแบ่งออกเป็นสองกรณีค่าฟังก์ชันสมบูรณ์ | | จะกำหนดโดย
ค่า absolute ของ x ให้ระยะห่างระหว่าง x และ 0 เป็นบวกหรือศูนย์เสมอ
ตัวอย่าง เช่น |3| = 3, |-3| = 3, |0|=0. | 3 | = 3, | -3 | = 3 | 0 | = 0
โดเมนของฟังก์ชันค่าสมบูรณ์คือ R ทั้งเส้นของจริงในขณะที่ช่วงคือช่วง [0, ∞)
ฟังก์ชันค่าสมบูรณ์สามารถอธิบายกฎ กราฟมันจะได้รับโดยสมการ y = กราฟเป็น Vดังรูป
ถ้า A และ B สองจุดบนเส้นจริงแล้วจากนิยามของ | x | เราดูอยู่ที่
ดังนั้น | a — b | แตกต่างกันขนาดใหญ่และขนาดเล็กของทั้งสองหมายเลขในคำอื่น ๆ | a — b | คือระยะระหว่างจุด A และ B, แสดงในรูป