คณิตศาสตร์เรื่องการแปลงทางเรขาคณิต   

1 การเลื่อนขนาน

2 การสะท้อน

3 การหมุน

การแปลงทางเรขาคณิต

การเลื่อนขนาน

คือ การเคลื่อนไหวของรูปเรขาคณิต โดย การเลื่อนขนาน การสะท้อน และการหมุนของรูปหนึ่งๆ พบได้ในสิ่งแวดล้อมรอบตัวเรา สามารถจำลองออกมาในรูปของการแปลง รวมทั้งงานศิลปะต่างๆ

มอริทส์ คอร์เนลิส เอสเซอร์ (Maurits Cornelis Escher)

เป็นศิลปินชาวดัทซ์ มีชื่อเสียงเรื่องแบบรูปที่ประสานกันโดยการทำซ้ำๆ เกิดจากการเปลี่ยนตำแหน่งโดยการเลื่อนขนาน (Translation) การหมุน (Rotation) การสะท้อน (Reflection) รวมเรียกว่า (Tessellation)ดังตัวอย่าง

การเลื่อนขนาน คือ การแปลงแบบหนึ่งที่จุดทุกจุดของรูปต้นแบบเคลื่อนไปในทิศทางเดียวกันเป็นระยะทางเท่าๆกัน จุดแต่ละจุดบนรูปที่ได้จากการเลื่อนขนานระยะห่างจากจุดที่สมนัยกันบนรูปต้นแบบเป็นระยะทางเท่ากันการเลื่อนใน ลักษณะนี้เรียกอีกอย่างหนึ่งว่า “สไลด์ (Slide)”

ในการเลื่อนขนานของรูปใดๆ จุดทุกจุดบนรูปจะเคลื่อนไปในแนวเส้นตรง และจุดทั้งหมดจะเคลื่อนไปในทิศทางเดียวกัน เป็นระยะทางเท่าๆกัน กับทางเดินของจุดนั้น

ในกรณีรูปที่ต้องการเลื่อนขนาน ถูกกำหนดเป็นคู่ลำดับที่อยู่ในระนาบมุมฉากต้องวาดรูปต้นแบบตามที่ถูกกำหนดก่อนแล้วเลื่อนขนาน วาดรูปจำลองไปทางซ้ายหรือลงข้างล่างเป็นลบ และไปทางขวาหรือขึ้นข้างบนเป็นบวก กับค่าพิกัด X และค่าพิกัด Y ของจุดยอดแต่ละจุดของรูปเดิม ผลลัพธ์คือ ค่าพิกัดของจุดยอดของรูปที่เลื่อนขนานแล้ว

ความหมายของการเลื่อนขนาน คือ ในด้านภาษา หมายถึง การเลื่อนขนานจุดหนึ่งจุดซึ่งแทนด้วยคู่อันดับให้บวกค่าพิกัดอันดับนั้นด้วยค่าพิกัดของจุด
ในด้านเลขคณิต หมายถึง (3,2) เคลื่อนไป (1,3) เป็น (4,5)
ในด้านพีชคณิต หมายถึง (x, y) เคลื่อนไป (a, b) เป็น (x + a ,y + b)
ตัวอย่างที่ 1 จุดยอดของรูป ANT คือ A(-4, 3), N(-6, 1) และ T(1, 0) จงสร้างรูป
ANT แล้ววาดรูปสามเหลี่ยมที่เกิดขึ้นจากการเลื่อนขนานไปทางขวา 3 หน่วย และลงล่าง 4 หน่วย

การสะท้อน เป็น การแปลงที่จุดทุกจุดของรูปต้นแบบเคลื่อนที่ข้ามเส้นตรงเส้นหนึ่ง ซึ่งเปรียบเสมือนกระจกหรือเรียกว่าเส้นสะท้อน (Reflection Line หรือ Mirror Line) โดยที่เส้นนี้จะแบ่งครึ่งและตั้งฉากกับส่วนของเส้นตรงที่เชื่อมระหว่างจุดแต่ละจุดบนรูปต้นแบบกับจุดแต่ละจุดบนรูปสะท้อนที่สมนัยกัน

การสะท้อนของจุดข้ามเส้น
ถ้ากำหนดจุดหนึ่งจุดเป็นจุด P การสะท้อนของจุดนั้นเรียกว่า รูปจำลองสะท้อนของจุด หรือ จุดสะท้อน P’ ซึ่งจะปรากฏอยู่ด้านตรงข้ามของเส้นสะท้อนด้วย ระยะห่างจากเส้นสะท้อนถึงจุด P’ เท่ากับระยะห่างจากเส้นสะท้อนถึงจุด P ดังรูป

การสะท้อนของรูปข้ามเส้นตรง

ถ้ากำหนดรูปใดรูปหนึ่งแล้ว การสะท้อนของรูปนั้น เรียกว่า รูปสะท้อน ซึ่งปรากฏอยู่ด้านตรงข้ามของเส้นสะท้อน และจุดทุกจุดของรูปสะท้อนมีระยะห่างจากเส้นสะท้อนเท่ากับระยะห่างจากเส้นสะท้อนถึงจุดแต่ละจุดแต่ละรูปบนรูปต้นแบบที่สมนัยกันดังรูป

การหมุน เป็น การแปลงที่จุดทุกจุดของรูปต้นแบบเคลื่อนที่ไปเป็นมุมเดียวกันรอบจุดตรึงอยู่กับที่ที่กำหนดหรือจุดหมุน
ในการหมุน (Rotation) รูปใดๆ จุดทุกจุดบนรูปจะเคลื่อนไปรอบๆ จุดที่กำหนด ซึ่งเรียกว่า จุดศูนย์กลางของการหมุน (Center of Rotation) โดยจุดทั้งหมดจะเคลื่อนที่เป็นมุมเดียวกัน

ความหมายของการสะท้อน

การสะท้อน

การสะท้อนบนระนาบเป็นการแปลงทางเรขาคณิตที่มีเส้นตรง l ที่ตรึงเส้นหนึ่งเป็นเส้นสะท้อน แต่ละจุด P บนระนาบจะมีจุด P’ เป็นภาพที่ได้จากการสะท้อนจุด P โดยที่

สมบัติของการสะท้อน

รูปเรขาคณิตที่สามารถหารอยพับและพับรูปทั้งสองข้างของรอยพับให้ทับกันสนิทได้เรียกว่า รูปสมมาตรบนเส้น และเรียกรอยพับนี้ว่า แกนสมมาตร รูปสมมาตรบนเส้นแต่ละรูปอาจมีจำนวนแกนสมมาตรไม่เท่ากัน

เส้นสะท้อน (แกนสมมาตร) จะแบ่งครึ่งและตั้งฉากกับส่วนของเส้นตรงที่เชื่อมระหว่างจุดแต่ละจุดบนรูปต้นแบบกับจุดแต่ละจุดบนรูปสะท้อนที่สมนัยกัน

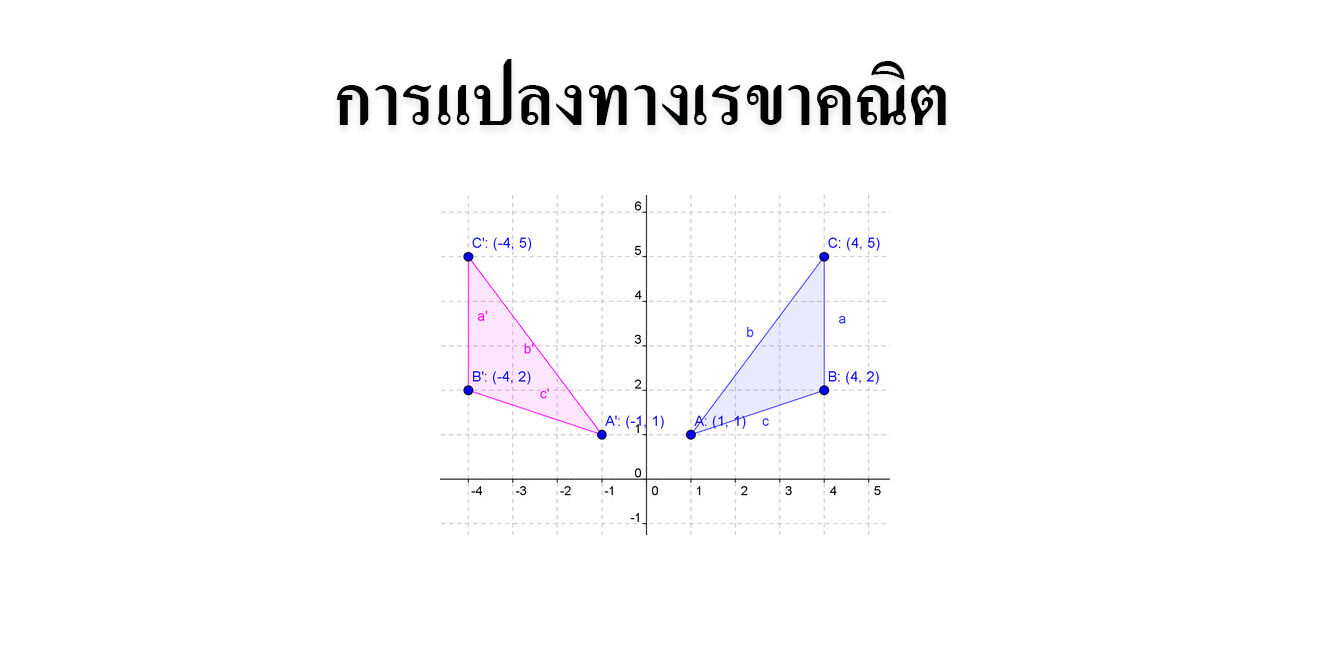
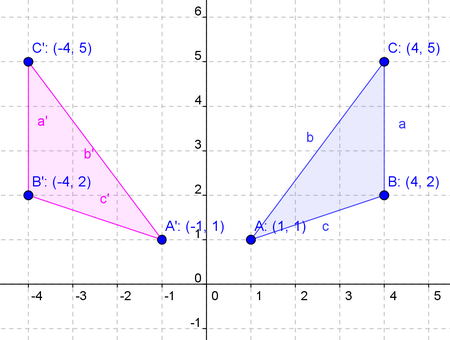
ถ้าเส้นสะท้อนเป็นแกน Y พิกัดของภาพที่เกิดจากการสะท้อน คือการเปลี่ยนเครื่องหมายของสมาชิกตัวหน้าเป็นเครื่องหมายตรงข้ามทุกจุดของรูปต้นแบบ ส่วนสมาชิกตัวหลังให้คงเดิมไว้

ถ้าเส้นสะท้อนเป็นแกน X พิกัดของภาพที่เกิดจากการสะท้อน คือการเปลี่ยนเครื่องหมายของสมาชิกตัวหลังเป็นเครื่องหมายตรงข้ามทุกจุดของรูปต้นแบบ ส่วนสมาชิกตัวหน้าให้คงเดิมไว้

ถ้าเส้นสะท้อนขนานแกน X หรือแกน Y ให้นับช่องตารางหาระยะระหว่างจุดที่กำหนดให้กับเส้นสะท้อนซึ่งภาพของจุดนั้นจะอยู่ห่างจากเส้นสะท้อนเป็นระยะที่เท่ากันกับระยะที่นับได้เมื่อได้ภาพของจุดนั้นแล้วจึงหาพิกัด

ถ้าเส้นสะท้อนไม่ขนานแกน X และไม่ขนานกับแกน Y แต่เป็นเส้นในแนวทแยง ให้ลากเส้นตรงผ่านจุดที่กำหนดให้และตั้งฉากกับเส้นสะท้อน ภาพของจุดที่กำหนดให้จะอยู่บนเส้นตั้งฉากที่สร้างขึ้นและอยู่ห่างจากเส้นสะท้อนเป็นระยะเท่ากันกับจุดที่กำหนดให้อยู่ห่างจากเส้นสะท้อน เมื่อได้ภาพของจุดนั้นแล้วจึงหาพิกัด

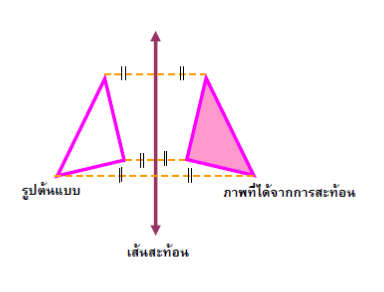
สมบัติการสะท้อน

สามารถเลื่อนรูปต้นแบบทับภาพที่ได้จากการสะท้อนได้สนิทโดยต้องพลิกรูปหรือกล่าวว่ารูปต้นแบบและภาพที่ได้จากการสะท้อนเท่ากันทุกประการ

1. ส่วนของเส้นตรงบนรูปต้นแบบและภาพที่ได้จากการสะท้อนของส่วนของเส้นตรงนั้นไม่จำเป็นต้องขนานกันทุกคู่
2. ส่วนของเส้นตรงที่เชื่อมจุดแต่ละจุดบนรูปต้นแบบกับจุดที่สมนัยกันบนภาพที่ได้จากการสะท้อนจะขนานกันและไม่จำเป็นต้องยาวเท่ากัน

การหมุน

การหมุนบนระนาบเป็นการแปลงทางเรขาคณิตที่มีจุด O เป็นจุดที่ตรึงอยู่จุดหนึ่งเรียกว่า O ว่า จุดหมุน แต่ละจุด P บนระนาบ มีจุด P’ เป็นภาพที่ได้จากการหมุนจุด P รอบจุด O ตามทิศทางที่กำหนดด้วยมุมที่มีขนาด K โดยที่

1. ถ้าจุด P ไม่ใช่จุด O แล้ว OP = OP^’ และขนาดของ  เท่ากับ K
2. ถ้าจุด P เป็นจุดเดียวกันกับจุด O แล้ว P เป็นจุดหมุน

สมบัติของการหมุน

1. สามารถเลื่อนรูปต้นแบบทับภาพที่ได้จากการหมุนได้สนิท โดยไม่ต้องพลิกรูปหรือกล่าวว่า รูปต้นแบบกับภาพที่ได้จากการหมุนเท่ากันทุกประการ
2. ส่วนของเส้นตรงบนรูปต้นแบบและภาพที่ได้จากการหมุนส่วนของเส้นตรงนั้นไม่จำเป็นต้องขนานกันทุกคู่ หรืออาจกล่าวได้ว่า จุดบนรูปต้นแบบและภาพที่ได้จากการหมุนจุดนั้น แต่ละคู่อยู่บนวงกลมเดียวกันและมีจุดหมุนเป็นจุดศูนย์กลาง แต่วงกลมเหล่านี้ไม่จำเป็นต้องมีรัศมียาวเท่ากัน

ลักษณะของการหมุน

การหมุนจะหมุนทวนเข็มหรือตามเข็มนาฬิกาก็ได้ จุดหมุนจะเป็นจุดที่อยู่บนรูปหรือนอกรูปก็ได้ โดยที่จุดแต่ละจุดบนรูปต้นแบบเคลื่อนที่รอบจุดหมุนด้วยขนานของมุมที่กำหนด

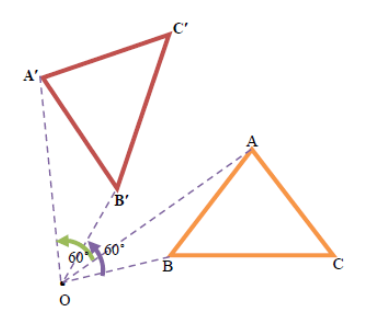
ตัวอย่าง กำหนดให้ ∆A’B’C’ เป็นภาพที่เกิดจากการหมุนรูป ∆ABC ตามเข็มนาฬิกาเป็นมุม 60 องศา โดยที่ A เป็นจุดหมุน และหมุนทวนเข็มนาฬิกาเป็นมุม 60 องศา โดยมีจุด O เป็นจุดหมุนที่ไม่อยู่บนรูปต้นแบบวิธีทำ
กรณีที่ A อยู่บนรูปต้นแบบและเป็นจุดหมุน
พิจารณาด้าน AC สร้างมุม CAC’ กาง 60 องศาในทิศตามเข็มนาฬิกา
แล้วลากด้าน AC’ ให้มีความยาวเท่ากับด้าน AC
ในทำนองเดียวกันสร้างมุม BAB’ กาง 60 องศา ในทิศตามเข็มนาฬิกา
และลากด้าน AB’ ให้มีความยาวเท่ากับด้าน AB แล้วลากด้าน B’C’
    กรณีที่จุดหมุน O ไม่อยู่บนรูปต้นแบบ ลากเส้น AO และ BO สร้างมุม AOA’ กาง 60 องศา ในทิศทวนเข็มนาฬิกา ลากเส้น OA’ ให้มีความยาวเท่ากับด้าน OA

ในทำนองเดียวกัน สร้างมุม BOB’ ทิศทวนเข็มนาฬิกากาง 60 องศา ลากเส้น OB’ ให้มีความยากเท่ากับด้าน AB ลากเส้นตรงเชื่อม B’C’