A-Level คณิต 1 : ความน่าจะเป็น
มีทั้งหมด 30 ข้อ คะแนนรวม 100 คะแนน
แบ่งเป็น 2 ตอน
ตอนที่ 1 แบบปรนัย มี 5 ตัวเลือก จำนวน 25 ข้อ
(ข้อ 1-25) ข้อละ 3 คะแนน รวม 75 คะแนน
ตอนที่ 2 แบบอัตนัย (เติมคำตอบ) จำนวน 5 ข้อ
(ข้อ 26-30) ข้อละ 5 คะแนน รวม 25 คะแนน
1. การนับจํานวนผลลัพธ์ทั้งหมดที่เกิดจากการกระทํา หรือการทดลองใดๆ ต้องอาศัยกฎเกณฑ์การนับจึงจะทําให้ง่ายและสะดวก รวดเร็ว
2. ความน่าจะเป็น คือ จํานวนที่แสดงให้ทราบว่าเหตุการณ์ใดเหตุการณ์หนึ่ง มีโอกาสเกิดขึ้นมาก หรือน้อยเพียงใด สิ่งที่จําเป็นต้องทราบทําความเข้้าใจ คือ
– การทดลองสุ่ม (Random Experiment)
– แซมเปิ้ลสเปซ (Sample Space)
– เหตุการณ์ (Event)
3. ความน่าจะเป็นของเหตุการณ์ใดๆ เป็นการเปรียบเทียบจํานวนสมาชิกของเหตุการณ์นั้นๆ กับ จํานวนสมาชิกของแซมเปิ้ลสเปซ ซึ่งเป็นค่าที่จะช่วยในการพยากรณ์หรือการตัดสินใจได์
ประกอบด้วยเนื้อหา ดังนี้
เรื่องที่ 1 กฎเบื้องต้นเกี่ยวกับการนับและแผนภาพต้นไม้
เรื่องที่ 2 ความน่าจะเป็นของเหตกุารณ์
ในชีวิตประจําวันของคนเรามีการกระทําหรือการทดลองหลายอย่างที่สามารถมีวิธีการที่จะเกิด ผลลัพธ์ได้หลายวิธี การหาจํานวนรูปแบบหรือจํานวนวิธทีี่อาจเกิดขึ้นได้จากการนับทั้งหมด โดยมีกฏเบื้องต้นเกี่ยวกับการนับ จากการทํางานดังนี้
สรุปขั้นตอนในการใช้กฎการนับแก้โจทย์ปัญหา
1. พิจารณาว่างานหรือเหตุการณ์ที่โจทย์กำหนดมานั้นคืออะไร จัดแบ่งออกเป็นกี่ขั้นตอนที่ต่อเนื่องกัน
2. พิจารณาเงื่อนไขต่าง ๆ ที่กําหนดมาในแต่ละขั้นตอน บันทึกไว้
3. หาจํานวนวิธีที่สามารเลือกทํางานได้ในแต่ละขั้น โดยต้องเริ่มจากขั้นที่มีเงื่อนไขมากที่สุดก่อนแล้วจึง พิจารณาขั้นอื่น ๆ ที่มีเงื่อนไขรองลงมา ตามความสําคัญ
4. นําจํานวนวิธีที่ได้ในแต่ละขั้นตอนคูณกัน จะได้จํานวนรูปแบบหรือจํานวนวิธีที่อาจเกิดขึ้นได้ทั้งหมด
ในชีวิตประจําวันมักพบกับการคาดคะเน หรือการประมาณเหตุการณ์ หรือโอกาส เพื่อใช้ในการ ตัดสินใจ โอกาสที่เหตุการณ์นั้น จะเกิดได้มีมากน้อยเพียงใด ขึ้นอยู่กับอัตราส่วนระหว่างจํานวนสมาชิก ของเหตุการณ์นั้น กับจํานวนครั้งของการทํางานผู้เรียนจึงต้องทราบ และทําความเข้าใจ กับคําเหล่านี้
1. การทดลองสุ่ม (Random Experiment) คือ การทดลองที่ไม่สามารถระบุผลลัพธ์ได้อย่างแน่นอน แต่บอกได้ว่าผลลัพธ์ของการทดลองนั้นมีโอกาสเกิดอะไรขึ้นได้บ้าง
ตัวอย่างที่ 1 การทดลองโยนลูกเต๋า 1 ลูก 1 ครั้ง แต้มที่จะเกิดขึ้นได้ คือ แต้ม 1, 2, 3, 4, 5 หรือ 6 ซึ่งไม่สามารถบอกได้ว่าจะเป็นแต้มอะไรใน 6 แต้มนี้
ดังนั้นผลลัพธ์ทั้งหมดที่จะเกดิขึ้นคือแต้ม 1, 2, 3, 4, 5, 6
ตัวอย่างที่ 2 การหยิบลูกปิงปอง 1 ลูก จากกล่อง ซึ่งมี 5 ลูก 5 สี ลูกปิงปองที่หยิบได้อาจจะเป็น ลูกปิงปอง สีขาว ฟ้า แดง เขียว หรือส้ม
ดังนั้นผลลัพธ์ทั้งหมดที่จะเกดิขึ้นคือ ลูกปิงปองสีขาว ฟ้า แดง เขียว หรือส้ม
ตัวอย่างที่ 3 จงเขียนผลที่อาจจะเกดิขึ้นได้ทั้งหมดในการโยนเหรียญบาท 1 เหรียญ และเหรียญห้าสิบ สตางค์ 1 เหรียญ
วิธีทํา ในการโยนเหรียญบาท 1 เหรียญ ผลที่อาจเกิดขึ้นคือหัวหรือก้อย
ถ้าให้ H แทน หัว และ ให้ T แทน ก้อย
ในการหาผลที่อาจเกิดขึ้นได้ทั้งหมดจากการโยนเหรยีญบาทและเหรียญห้าสิบสตางค์อย่างละ 1 เหรียญ อาจใช้แผนภาพช่วยได้ดังนี้
ฉะนั้น ถ้าเราใช้คู่อันดับเขียนผลทั้งหมดที่อาจเกิดขึ้นได้โดยให้สมาชิกตัวหนึ่งของคู่อันดับแทนผล ที่อาจเกิดขึ้นจากเหรียญบาท สมาชิกตัวที่สองของคู่อันดับแทนผลที่อาจเกิดขึ้นจากเหรียญห้าสิบ สตางค์ จะได้ ผลทั้งหมดที่อาจจะเกิดขึ้นได้ คือ (H, H), (H, T), (T, H) และ (T, T)
2. แซมเปิ้ลสเปซ (Sample Space ) เป็นเซตที่มีสมาชิกประกอบด้วยสิ่งที่ต้องการ ทั้งหมด จากการ ทดลองอย่างใดอย่างหนึ่ง ( บางครั้งเรียกว่า Universal Set ) เขียนแทนด้วย S
เช่น ตัวอย่างที่ 4 ในการโยนลูกเต๋าถ้าต้องการดูว่าหน้าอะไรจะขนึ้มาจะได้ ผลลัพธ์ที่อาจจะเกิดขึ้นได้คือ ลูกเต๋าขึ้นแต้ม 1 หรือ 2 หรือ 3 หรือ 4 หรือ 5 หรือ 6
ดังนั้นแซมเปิ้ลสเปซที่ได้ คือ S = { 1, 2, 3, 4, 5, 6 }
ตัวอย่างที่ 5 จากการทดลองสุ่มโดยการทดลองทอดลูกเต๋า 2 ลูก
1. จงหาแซมเปิ้ลสเปซของแต้มของลูกเต๋าที่หงายขึ้น
วิธีทํา 1. เนื่องจากโจทย์สนใจแต้มของลูกเต๋าที่หงายขึ้น ดังนั้นเราต้องเขียนแต้มของลูกเต๋าที่มีโอกาส ที่จะหงายขึ้นมาทั้งหมด และเพื่อความสะดวกให้ (a , b) แทนผลลัพธ์ที่อาจจะเกิดขึ้น
โดยที่ a แทนแต้มที่หงายขึ้นของลูกเต๋าลกูแรก
b แทนแต้มที่หงายขึ้นของลูกเต๋าลูกที่สอง
ดังนั้นแซมเปิ้ลสเปซของการทดลองสุ่มคือ
S = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}
3. เหตุการณ์ (event) คือ เซตที่เป็นสับเซตของ Sample Space หรือเหตุการณ์ที่เราสนใจ จากการทดลองสุ่ม
ตัวอย่างที่ 6 ในการโยนลูกเต๋า 1 ลูก 1 ครั้ง ถ้าผลลัพธ์ที่สนใจคือ จํานวนแต้มที่ได้ จะได้
S = {1, 2, 3, 4, 5, 6}
ถ้าให้ E1 เป็นเหตุการณ์ที่ได้แต้มซึ่งหารดว้ย 3 ลงตัว จะได้ E1 = {3, 6} E2 เป็นเหตุการณ์ที่ได้แต้มมากกว่า 2 จะได้ E2 = {3, 4, 5, 6}
4. ความน่าจะเป็นของเหตุการณ์
ความน่าจะเป็นของเหตกุารณ์ คือ จํานวนที่แสดงให้ทราบว่าเหตุการณ์ใดเหตุการณ์หนึ่งมีโอกาส เกิดขึ้นมากหรือน้อยเพียงใด
ความน่าจะเป็นของเหตุการณ์ใด ๆ เท่ากับอัตราส่วนของจํานวนเหตุการณ์ที่เราสนใจ (จะให้เกิดขึ้น หรือไม่เกิดขึ้นก็ได้) ต่อจํานวนผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ ซึ่งมีสูตรในการคิดคํานวณดังนี้
เมื่อผลทั้งหมดที่อาจจะเกิดขึ้นจากทดลองสุ่มแต่ละตัวมีโอกาสเกิดขึ้นได้เท่าๆ กัน
กําหนดให้ E แทน เหตุการณ์ที่เราสนใจ
P(E) แทน ความน่าจะเป็นของเหตุการณ์
n(E) แทน จํานวนสมาชกิของเหตุการณ์
n(S) แทน จํานวนสมาชิกของผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้
ความน่าจะเป็นของเหตุการณ์
คำว่า “ความน่าจะเป็น” หรือ “probability” เป็นวิธีการวัดความไม่แน่นอนในรูปแบบคณิตศาสตร์ เช่น เมื่อโยนเหรียญ ความน่าจะเป็นของเหรียญที่จะออกหัวหรือก้อยเท่ากับ 0.5
ดังนั้นเหตุการณ์ต่าง ๆ ที่เกิดขึ้นในอาณาคตเป็นสิ่งที่ยากจะคาดเดาได้ถูกต้องร้อยเปอร์เซนต์ นักอุตุนิยมวิทยาจึงใช้หลักการของความน่าจะเป็นเข้ามาทำนาย เช่น ความน่าจะเป็นของการเกิดฝนตกใน กรุงเทพมหานคร ในวันพรุ่งนี้มีค่าเท่ากับ 0.7
เราจะวัดหาค่าความน่าจะเป็นได้อย่างไร
ความน่าจะเป็น เป็นค่าที่อาจมีความหมายที่หลายคนเข้าใจได้ไม่ยาก ความน่าจะเป็น เป็นศาสตร์ที่มีความละเอียดอ่อนที่จะนำไปประยุกต์ใช้ โดยเฉพาะเหตุการณ์ในชีวิตประจำวันต่าง ๆ ความน่าจะเป็นมีการกำหนดค่าเป็นเศษส่วนหรือเป็นเปอร์เซนต์หรือให้มีค่าระหว่าง 0 ถึง 1 เช่น ถ้านำลูกเต๋า ทอยลงบนพื้น โอกาสที่จะปรากฎหน้า 1 มีค่าเท่ากับ 1/6 หรือ 16.6 เปอร์เซนต์ ถ้าโยนเหรียญหนึ่งเหรียญ และให้ตกบนพื้น (โยนแบบยุติธรรม) โอกาสที่จะปรากฏหัวเท่ากับ 1/2 หรือ 0.5
เราสามารถวัดหาค่าความน่าจะเป็นได้สองวิธี (บางทีเป็น 3 วิธี) ขึ้นกับสภาวะแวดล้อม
-
- เมื่อเหตุการณ์ปรากฏมีลักษณะเหมือน ๆ กัน
- เมื่อเหตุการณ์ที่เกิดขึ้นมีลักษณะไม่เหมือนกันตามสิ่งแวดล้อม
เมื่อเหตุการณ์ปรากฏมีลักษณะเหมือน ๆ กัน
สมมุติว่าเราทอยเหรียญจะมีโอกาสที่เป็นไปได้สองแบบคือ หัว หรือก้อย ถ้าเหรียญเป็นเหรีญญปกติ การทอยทอยอย่างยุติธรรม ผลที่เกิดหัวหรือก้อยมีลักษณะเท่าเทียมกัน
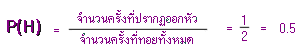
ทำนองเดียวกันที่เราทอยลูกเต๋า โอกาสที่ลูกเต๋าจะปรากฎหน้า 1, 2, 3, 4, 5 และ 6 มีได้เท่ากัน ดังนั้น ความน่าจะเป็นของการทอยลูกเต๋าให้ปรากฎหน้าที่เป็นเลขคู่
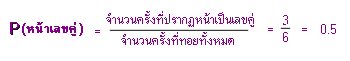
ประชากรคนไทยยังนิยมการเสี่ยงโชค รัฐบาลได้ออกฉลากกินแบ่งหรือที่รู้จักกันในนามลอตเตอรี่ หรือ หวยรัฐบาล ตัวเลขของฉลากกินแบ่ง มี 6 ตัวเลข ซึ่งก็มีจำนวนฉลากทั้งสิ้น 1 ล้าน ฉบับ มีรางวัลที่หนึ่งมี 1 รางวัล รางวัลที่สอง มี 5 รางวัล รางวัลที่สามมี 10 รางวัล รางวัลที่สี่มี 50 รางวัล รางวัลที่ห้ามี 100 รางวัล
โอกาสที่จะถูกรางวัลที่หนึ่ง คือ
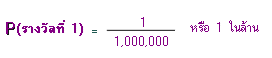
โอกาสที่จะถูกรางวัลที่ 1 ถึง 5 มี
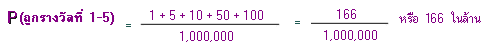
ดังนั้นถ้าเหตุการณ์ที่ปรากฎแต่ละครั้งมีโอกาสเท่าเทียมกับสิ่งที่เป็นความน่าจะเป็นคือ
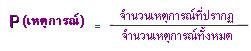
ลักษณะที่กล่าวมานี้เห็นว่าโอกาสหรือสิ่งที่เป็นเหตุการณ์แต่ละครั้งที่ปรากฎ จะมีโอกาสความน่าจะเป็นเท่ากัน ลักษณะจึงเหมือนการทอยเหรียญ ลูกเต๋า หรือการซื้อลอตเตอรี่ ทุกครั้งที่มีเหตุการณ์เกิดขึ้นขึงมีความน่าจะเป็นที่ชัดเจน
เมื่อเหตุการณ์ที่เกิดขึ้นมีลักษณะไม่เหมือนกันตามสิ่งแวดล้อม
เมื่อเหตุการณ์ที่เกิดขึ้นมีลักษณะไม่เหมือนกันตามสิ่งแวดล้อม การกล่าวถึงเหตุการณ์ที่ปรากฎาขึ้นมาแต่ละครั้งของการทอยเหรียญถือว่าโอกาสของเหรียญก็ยังคงเท่าเดิมทุกครั้ง แต่ถ้าเปรียบเทียบกับการเลือกตั้งในประเทศไทย สมมุติว่ามีพรรคการเมืองใหญ่ เช่น ประชาธิปัตย์ ความหวังใหม่ กิจสังคม ชาติไทย ชาติพัฒนา และประชากรไทย โอกาสของการเลือกตั้งของแต่ละพรรคในการได้ สส. เมื่อเวลาเปลี่ยนไปสิ่งแวดล้อมเปลี่ยนไป ความน่าจะเป็นก็จะเปลี่ยนไปด้วย ซึ่งผิดกับการทอยเหรียญเมื่อเวลาใดก็ยังคงได้ความน่าจะเป็นคงที่
หรือดูจากนักเรียนที่กำลังนั่งทำข้อสอบวิชาคณิตศาสตร์ มีความน่าจะเป็นที่จะสอบได้ และสอบตกอย่างไร สิ่งที่เป็นผลของเหตุการณ์นี้ขึ้นกับความขยันและความตั้งใจเรียนของนักเรียนผู้นี้ หากช่วงเวลาที่ผ่านมามีความสนใจเรียน ดูหนังสือสม่ำเสมอ ความน่าจะเป็นในการที่จะสอบได้ก็มีสูง หรืออาจจะเท่ากับ 1 เลยก็ได้ แต่ถ้าไม่สนใจเรียนหนังสือและไม่ได้เตรียมตัวมาสอบให้ดี ความน่าจะเป็นในการสอบได้ ก็อาจจะเข้า
เมื่อเหตุการณ์ที่เกิดขึ้นแต่ละครั้งอาจแตกต่างกัน การวัดค่าความน่าจะเป็นทำได้อย่างไร จากหลักการทางทฤษฎีเราก็ยังคงวัดจากเหตุการณ์ในอดีต และหาตัวเลขของความน่าจะเป็น เช่น โรงงานผลิตช่างอิเล็กทรอนิกส์จำพวกไอซี มีเครื่องจักรหลายเครื่อง วิชาการสนใจสภาพเครื่องจักรหมายเลข 8 จึงทำการเก็บตัวอย่างจำนวนการผลิตทั้งหมดที่ผลิตผ่านเครื่องจักรนี้ จำนวน 8000 ชิ้น เมื่อตรวจสอบพบว่ามีชิ้นส่วนที่เสียอยู่ 80 ชิ้น
![]()
จะเห็นว่าเครื่องจักรนี้ผลิตขึ้นส่วนอิเล็กทรอนิกส์นี้ มีความน่าจะเป็นในการผลิตของเสีย 0.01 และถ้ามีการปรับปรุงเครื่องจักร จำนวนชิ้นที่เสียก็น่าจะลดลงไปได้
บริษัทแห่งหนึ่งรับโทรศัพท์จำนวน 1000 ครั้งในรอบหนึ่งปี ปรากฏว่าพนักงานได้จดบันทึกทุกครั้ง เมื่อแยกแยะพบว่าเป็นการโทรศัพท์ติดต่อเรื่องเกี่ยวกับการขาย 150 ครั้ง ความน่าจะเป็นของการโทรศัพท์เข้ามาติดต่อในเรื่องการขายหาได้จาก
![]()






