กราฟ-ทฤษฎีกราฟเบื้องต้นกราฟ
อาจจะได้แผนภาพดังนี้
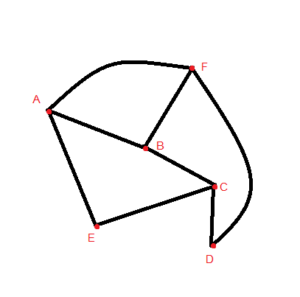
สมมติ ว่าจังหวัดหนึ่งมี 6 อำเภอ คือ A , B , C , D , E และ F
โดยที่อำเภอ A , B และ F มีถนนเชื่อมติดต่อกัน
อำเภอ C มีถนนเชื่อมไปยังอำเภอ B , E และ D
อำเภอ A และ E มีถนนเชื่อมติดต่อกัน
และอำเภอ D และ F มีถนนเชื่อมติดต่อกัน
เขียนแผนภาพโดยให้จุดแทนอำเภอและเส้น เชื่อมโยงระหว่างจุดสองจุดแทนถนน
เรียกแผนภาพซึ่งประกอบด้วยจุดและเส้นในลักษณะนี้ว่า “กราฟ (graph)”
จากแผนภาพในรูปที่ 1 จะสังเกตเห็นว่า “กราฟ” ที่จะศึกษาในบทนี้ ไม่ได้หมายถึงกราฟของความสัมพันธ์หรือกราฟของฟังก์ชัน ในที่นี้ “กราฟ” เป็นแผนภาพที่ประกอบด้วยจุดและเส้นที่เชื่อมระหว่างจุด
จากแผนภาพในรูปที่ 1 เรียกจุด A, B, C, D, E, และ F ว่า ”จุดยอด” และเรียกเส้นที่เชื่อมระหว่างจุดยอดสองจุดว่า “เส้นเชื่อม” เส้นที่เชื่อมอาจเป็นส่วนของเส้นตรงหรือเส้นโค้งก็ได้
ในเชิงคณิตศาสตร์”กราฟ” มีบทนิยามดังนี้
บทนิยาม กราฟ G ประกอบด้วย เซตจำกัด 2 เซต คือ
1. เซตที่ไม่เป็นเซตว่างของจุดยอด (Vertex) แทนด้วยสัญลักษณ์ V (G)
2. เซตของเส้นเชื่อม (Edge) ที่เชื่อมระหว่างจุดยอด
แทนด้วยสัญลักษณ์ E (G)
ข้อสังเกต V(G) ≠ ∅ แต่ E(G) อาจเป็นเซตว่างได้
ตัวอย่างที่ 1 กำหนดกราฟ G ดังรูป
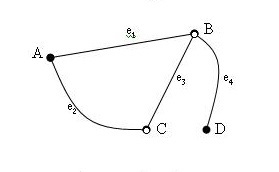
จากกราฟ G ที่กำหนดให้ จะได้ว่า
V(G) = {A , B , C , D}
E(G) = {e1 , e2 , e3 , e4 } หรือ
E(G) = {AB , AC , BC , BD}
หมายเหตุ
1. ในการเขียนกราฟนั้น จะต้องกำหนดตำแหน่งของจุดยอด ณ ตำแหน่งใดก็ได้ และจะลากเส้นเชื่อมของกราฟเป็นส่วนของเส้นตรงหรือเส้นโค้ง มีความยาวเป็นเท่าใดก็ได้ เช่น กราฟต่อไปนี้ ถือว่าเป็นกราฟเดียวกัน
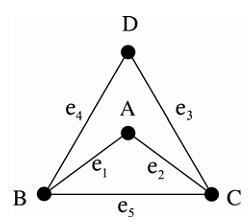
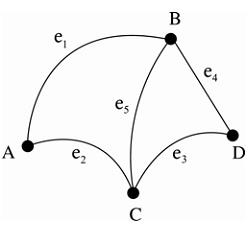
2. เส้นเชื่อมสองเส้นของกราฟ อาจลากตัดกันได้โดยที่จุดตัดของเส้นตรงทั้งสองไม่ถือว่าเป็นจุดยอดของกราฟ เช่น
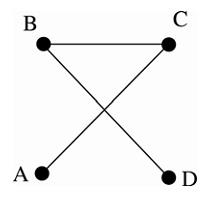
สามารถเขียนโดยมีเส้นเชื่อมไม่ตัดกันดังนี้
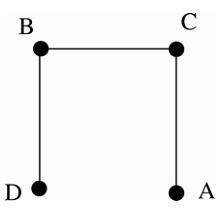
กำหนดกราฟดังรูป
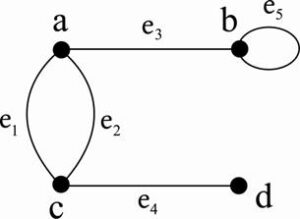
จากรูป จะเห็นว่า e1 และ e2 เป็นเส้นเชื่อมระหว่างจุดยอดคู่เดียวกัน คือ จุดยอด a และจุดยอด c
เส้น e5 เป็นเส้นเชื่อมที่เชื่อมจุดยอด b เพียงจุดเดียว
บทนิยาม เส้นเชื่อมตั้งแต่ 2 เส้นที่เชื่อมระหว่างจุดยอดคู่เดียวกัน เรียกว่า เส้นเชื่อมขนาน (Parallel
Edges) เส้นเชื่อมที่เชื่อมจุดยอดเพียงจุดเดียว เรียกว่า วงวน (Loop)
จากรูปข้างต้นจะเห็นว่า
e1 และ e2 เป็น เส้นเชื่อมขนาน
เส้นเชื่อม e5 เป็นวงวน
ในกรณีที่กราฟไม่มีเส้นเชื่อมขนาน สามารถใช้สัญลักษณ์ AB เพื่อแทนเส้นเชื่อมระหว่างจุดยอด A และ B ได้ เช่น กราฟในตัวอย่างที่ 1 สามารถเขียนเซตของเส้นเชื่อม E(G) ได้ใหม่เป็น
E(G) = {AB, BC, AC, CD}
ตัวอย่างต่อไปนี้เป็นตัวอย่างของแบบจำลองของสถานการณ์ต่างๆด้วยกราฟ
ตัวอย่างที่ 2 สมมุติว่าตำแหน่งงาน 4 ตำแน่ง คือ A, B, C และ D และมีผู้สมัครงาน 4 คน คือ ก, ข, ค, และ ง โดยที่แต่ละคนมีความสามารถทำงานในตำแหน่งต่างๆ ดังนี้
ก มีความสามารถทำงานในตำแหน่งงาน A
ข มีความสามารถทำงานในตำแหน่งงาน A , B และ D
ค มีความสามารถทำงานในตำแหน่งงาน C และ D
ง มีความสามารถทำงานในตำแหน่งงาน A และ B
ต้องการมอบหมายงานให้กับผู้สมัครงานทั้งสี่คน โดยที่แต่ละคนได้ทำงานตามความสามารถในตำแหน่งงาน
เพียง 1 ตำแหน่ง
วิธีทำ จำลองปัญหานี้ด้วยกราฟ G โดยที่
V(G) = {A, B, C, D, ก, ข, ค, ง} และ
E(G) = {กA, ขA, ขB, ขD, คC, คD, งA, งB}
แสดงแผนภาพของกราฟ G ได้ดังรูป
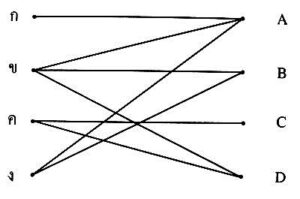
ตัวอย่างหนึ่งของการมอบหมายงานให้กับผู้สมัครทั้งสี่คนเป็นดังนี้
ก ทำงานในตำแหน่งงาน A
ข ทำงานในตำแหน่งงาน D
ค ทำงานในตำแหน่งงาน C
ง ทำงานในตำแหน่งงาน B
ตัวอย่างที่ 3 ในการจัดตารางสอบของวิชา 6 วิชา คือ วิชาคณิตศาสตร์ วิชาภาษาอังกฤษ วิชาภาษาไทย วิชาวิทยาศาสตร์ วิชาสังคมศึกษา และวิชาสุขศึกษา โดยที่ทราบว่า
มีนักเรียนบางคนเรียนวิชาคณิตศาสตร์และวิชาภาษาอังกฤษ
มีนักเรียนบางคนเรียนวิชาคณิตศาสตร์และวิชาภาษาไทย
มีนักเรียนบางคนเรียนวิชาคณิตศาสตร์และวิชาสุขศึกษา
มีนักเรียนบางคนเรียนวิชาสุขศึกษาและวิชาภาษาสังคมศึกษา
มีนักเรียนบางคนเรียนวิชาสังคมศึกษาและวิชาวิทยาศาสตร์
มีนักเรียนบางคนเรียนวิชาวิทยาศาสตร์และวิชาภาษาไทย
มีนักเรียนบางคนเรียนวิชาภาษาอังกฤษและวิชาภาษาไทย
จะสามารถจัดตารางสอบทั้งหกวิชา โดยใช้เวลา 3 คาบ ได้อย่างไร
วิธีทำ จำลองปัญหาด้วยกราฟโดยให้จุดยอดแทนวิชา และจุดยอดสองจุดมีเส้นเชื่อมก็ต่อเมื่อมีนักเรียนบางคนเรียนทั้งสองวิชา ดังรูป
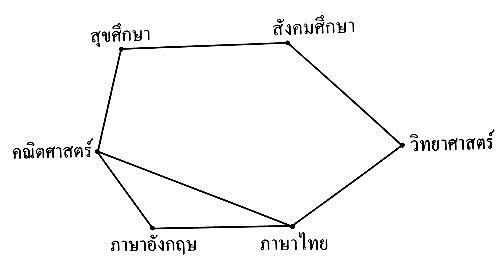
จากแผนภาพของกราฟ แสดงว่าจัดสอบวิชาคณิตศาสตร์ วิชาภาษาไทย และวิชาภาษาอังกฤษ ในคาบเวลาเดียวกันไม่ได้ แต่วิชาคณิตศาสตร์และวิชาสังคมศึกษา หรือ วิชาคณิตศาสตร์และวิชาวิทยาศาสตร์ สามารถจัดในคาบเวลาเดียวกันได้
ดังนั้นการจัดเวลาสอบให้ได้แต่ละวิชากระทำได้ดังนี้
ถ้าจุดยอด 2 จุดมีเส้นเชื่อมจะจัดสอบในคาบเวลาต่างกัน
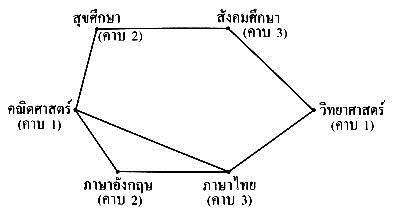
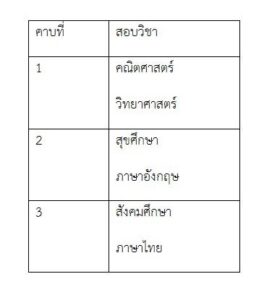
ตัวอย่างหนึ่งในการจัดสอบวิชาทั้งหกวิชา เป็นดังนี้
นักเรียนลองจัดตารางสอบทั้ง 6 วิชา ในรูปแบบอื่นๆ โดยใช้เวลา 3 คาบ
บทนิยาม จุดยอด u และจุดยอด v ของกราฟ เป็นจุดยอดประชิด (Adjacent Vertices)
ก็ต่อเมื่อ มีเส้นเชื่อมระหว่างจุดทั้งสอง และเราเรียกจุดยอด u และ v ว่า จุดปลาย
(End Point)ของเส้นเชื่อมนั้น
เส้นเชื่อม e ของกราฟ เกิดกับ (Incident)จุดยอด v ถ้าจุดยอด v เป็นจุดปลายจุด หนึ่งของเส้นเชื่อม
ตัวอย่าง กำหนดกราฟ ดังรูป
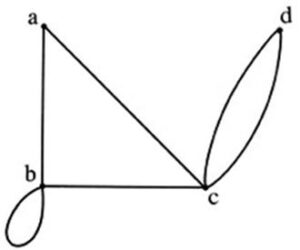
จากรูป จะเห็นว่า
จุดยอด a และจุกยอด b เป็นจุดยอดประชิด
จุดยอด a และจุกยอด d เป็นจุดยอดประชิด
จุดยอด b และจุกยอด c เป็นจุดยอดประชิด
จุดยอด c และจุกยอด d เป็นจุดยอดประชิด
จุดยอด c และจุกยอด e เป็นจุดยอดประชิด
แต่จุดยอด a และจุดยอด e ไม่เป็นจุดยอดประชิด
และจุดยอด a และจุดยอด c ไม่เป็นจุดยอดประชิด
และ จะเห็นว่า
เส้นเชื่อมที่เกิดกับจุดยอด a คือ ab และ ad
เส้นเชื่อมที่เกิดกับจุดยอด b คือ ba และ bc
เส้นเชื่อมที่เกิดกับจุดยอด c คือ cb , ce และ cd
เส้นเชื่อมที่เกิดกับจุดยอด c คือ da และ dc
เส้นเชื่อมที่เกิดกับจุดยอด e คือ ec






