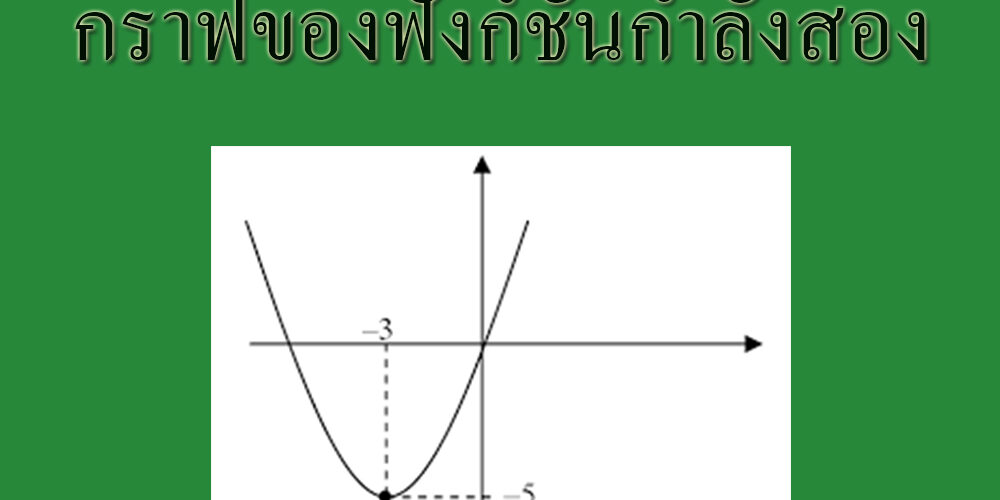
กราฟของฟังก์ชันกำลังสอง
เรื่องแนะนำฟังก์ชัน และ กราฟของฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง (Quadratic function)
ฟังก์ชันกำลังสองเป็นฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a, b, c เป็นจำนวนจริงใด ๆ และ a ¹ 0 ซึ่งกราฟของฟังก์ชันกำลังสอง เรียกว่า พาราโบลา
1) y = 2x2 + 3x – 10 เมื่อ a = 2 , b = 3 และ c = -1
2) y = x2 + 1 เมื่อ a = 1 , b = 0 และ c = 1
3) y = -x2 + 2x + 1 เมื่อ a = -1 , b = 2 และ c = 1
1) กราฟของฟังก์ชันกำลังสอง ที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0
กราฟของฟังก์ชันกำลังสอง มีชื่อเรียกว่า พาราโบลา ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ a , b และ c และเมื่อ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0 เมื่อ a > 0 และชนิดคว่ำ เมื่อ a < 0
ก ราฟของฟังก์ชันกำลังสอง
ฟังก์ชัน (function) คือ ความสัมพันธ์ของปริมาณ x และปริมาณ y โดยที่ปริมาณ x แต่ละค่าจะมี
ปริมาณ y ที่สอดคล้องกันเพียง 1 ค่า
ข้อตกลงเกี่ยวกับสัญลักษณ์
กรณีที่ f เป็นฟังก์ชัน และค่าของ y ขึ้นอยู่กับค่าของ x จะเขียนแทนด้วย y = f(x) และเรียก f(x) ว่า
ค่าของฟังก์ชัน f ที่ x
สัญลักษณ์ f(x) อ่านว่า “เอฟของเอกซ์” หรือ “เอฟเอ็กซ์”
ตัวอย่างที่ 1
จงตรวจสอบว่าความสัมพันธ์ต่อไปนี้เป็นฟังก์ชันหรือไม่
1) y = x2 + 3x
วิธีทำ เนื่องจาก เมื่อแทนค่า x ด้วยจำนวนจริงใด ๆ แต่ละค่าของ x จะให้ค่าเพียง 1 ค่า
เช่น เมื่อแทนค่า x ด้วย 0 จะได้ y = 0 2 + 3(0) = 0
เมื่อแทนค่า x ด้วย 1 จะได้ y = 1 2 + 3(1) = 4
เมื่อแทนค่า x ด้วย 2 จะได้ y = 2 2 + 3(2) = 10
ดังนั้น ความสัมพันธ์ y = x2 + 3x เป็นฟังก์ชัน
2) x = (y + 1)2 เด็ก ๆ จำง่าย คือ
เมื่อแทนค่า x 1 ค่า
วิธีทำ เนื่องจาก เมื่อแทนค่า x ด้วย 1 จะได้ 1 = (y + 1)2 แล้วจะต้องได้ค่า y 1 ค่า
จึงจะเป็นฟังก์ชัน
นั่นคือ y + 1 = 1 หรือ y + 1 = -1
จะได้ y = 0 หรือ y = -2
จะพบว่า ค่า x 1 ค่า จะทำให้ได้ค่า y 2 ค่า
ดังนั้น ความสัมพันธ์ x = (y + 1)2 ไม่เป็นฟังก์ชัน
รายวิชา คณิตศาสตร์5 ค23101 : กราฟของฟังก์ชันกำลังสอง โดย ครูวินัญญา เณรภักดี 1
ตัวอย่างที่ 2
ให้ f(x) = x2 – x + 5 แล้ว f(2) + f(3) – f(4)
วิธีทำ
จาก f(x) = x2 – x + 5
จะได้ f(2) = 22 – 2 + 5 = 4 – 2 + 5 = 7
f(3) = 32 – 3 + 5 = 9 – 3 + 5 = 11
f(4) = 42 – 4 + 5 = 16 – 4 + 5 = 17
ดังนั้น f(2) + f(3) – f(4) = 7 + 11 – 17 = 1
ตอบ 1
2 กราฟของฟังก์ชันกำลังสอง
2 ฟังก์ชันกำลังสอง (Quadratic Function) จะอยู่ในรูป y = ax + bx + c หรือ f(x) = ax + bx + c
เมื่อ a, b และ c เป็นค่าคงตัว และ a ≠ 0 โดยสมการ y = ax2 + bx + c เรียกว่า สมการของพาราโบลา
สมการของพาราโบลา ≠a 0 เพราะ…?
สมการที่เขียนอยู่ในรูป y = ax2 + bx + c ถ้า a = 0 จะทำให้สมการเป็น
เมื่อ x และ y เป็นตัวแปร y = bx + c
a, b และ c เป็นค่าคงตัว และ a ≠ 0 ซึ่งเป็น สมการเส้นตรง
ไม่ใช่พาราโบลา
ส่วนประกอบของพาราโบลา
ส่วนประกอบที่นักเรียนควรรู้จักในระดับชั้นมัธยมศึกษาตอนต้น
จุดยอด (จุดวกกลับ) มี 2 แบบ คือ กราฟหงาย : จุดยอด เป็น จุดต่ำสุด
กราฟคว่ำ : จุดยอด เป็น จุดสูงสุด
แกนสมมาตร คือ แกนที่แบ่งพาราโบลาออกเป็นสองส่วนเท่า ๆ กัน
รายวิชา คณิตศาสตร์5 ค23101 : กราฟของฟังก์ชันกำลังสอง โดย ครูวินัญญา เณรภักดี 2
จุดตัดแกน X , จุดตัดแกน Y
Y a>0 จุดยอด Y a<0
(จุดสูงสุด)
แกนสมมาตร จุดตัดแกน Y
จุดตัดแกน X
จุดยอด แกนสมมาตร
(จุดต่ำสุด) จุดตัดแกน Y
พาราโบลาหงาย พาราโบลาคว่ำ
กราฟของพาราโบลาจากรูปแบบสมการต่าง ๆ
1สมการรูปแบบที่ y = ax2
พาราโบลาหงาย (a > 0) พาราโบลาหงาย (a < 0)
ฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง คือ ฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ a ≠ 0 ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ

จากรูปจะเห็นว่า ถ้า a > 0 กราฟเป็นเส้นโค้งหงายขึ้น
a < 0 กราฟเป็นเส้นโค้งคว่ำลง
กราฟของฟังก์ชันกำลังสองในรูปนี้มีชื่อว่า พาราโบลา
ในกรณีทั่วไป กราฟของ y = a(x-h)2 + k , a ≠ 0 จะมีจุดที่กราฟวกกลับดังนี้
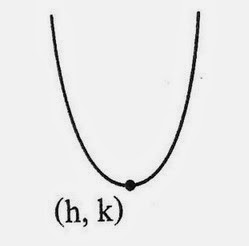
f(x) = a(x-h)2 + k , a > 0
จากรูปกราฟของ f มีจุดวกกลับที่จุด (h,k) ซึ่งเป็นจุดที่ f(x) มีค่าต่ำสุด และ f(h) = k เป็นค่าต่ำสุดของ f
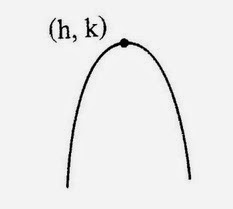
f(x) = a(x-h)2 + k , a < 0
จากรูปกราฟของ f มีจุดวกกลับที่จุด (h,k) ซึ่งเป็นจุดที่ f(x) มีค่าสูงสุด และ f(h) = k เป็นค่าสูงสุดของ f