ลอการิทึมธรรมชาติของตัวเลขเป็นของลอการิทึมไปยังฐานของค่าคงที่ทางคณิตศาสตร์ อีที่อีเป็นไม่ลงตัวและยอดเยี่ยมจำนวนประมาณเท่ากับ2.718 281 828 459 ลอการิทึมธรรมชาติของ xถูกเขียนโดยทั่วไปเป็น LN x ,เข้าสู่ระบบ_E xหรือบางครั้งถ้าฐานอีเป็นนัยเพียงเข้าสู่ระบบ x  วงเล็บมีการเพิ่มบางครั้งเพื่อความชัดเจนให้ LN ( x ) ,เข้าสู่ระบบ_E ( x )หรือเข้าสู่ระบบ ( x ) สิ่งนี้ทำได้โดยเฉพาะเมื่ออาร์กิวเมนต์ของลอการิทึมไม่ใช่สัญลักษณ์เดียวเพื่อป้องกันความคลุมเครือ

 

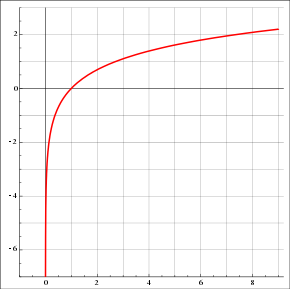
กราฟของฟังก์ชันลอการิทึมธรรมชาติ ฟังก์ชันค่อยๆเติบโตเป็นอินฟินิตี้ที่เป็นบวกเมื่อ xเพิ่มขึ้นและค่อยๆไปที่อินฟินิตี้เชิงลบเมื่อ xเข้าใกล้ 0 (“ช้า” เมื่อเทียบกับกฎกำลังของ xใด ๆ ); Yแกนเป็น สิ้นสุด

ลอการิทึมธรรมชาติของxเป็นพลังที่อีจะต้องถูกยกขึ้นไปเท่ากับx ยกตัวอย่างเช่นLN 7.5เป็น2.0149 …เพราะอี^{2.0149 …} = 7.5 ลอการิทึมธรรมชาติของอีตัวเองLN อีเป็น1เพราะE ¹ = อีขณะที่ลอการิทึมธรรมชาติของ1เป็น0ตั้งแต่อี⁰ = 1

ลอการิทึมธรรมชาติสามารถกำหนดให้กับจำนวนจริง บวกaเป็นพื้นที่ใต้เส้นโค้ง y = 1 / xจาก1ถึงa  (โดยพื้นที่เป็นลบเมื่อ0 < a <1 ) ความเรียบง่ายของคำจำกัดความนี้ซึ่งตรงกับสูตรอื่น ๆ อีกมากมายที่เกี่ยวข้องกับลอการิทึมธรรมชาตินำไปสู่คำว่า “ธรรมชาติ” จากนั้นคำจำกัดความของลอการิทึมธรรมชาติสามารถขยายได้เพื่อให้ค่าลอการิทึมสำหรับจำนวนลบและสำหรับจำนวนเชิงซ้อนที่ไม่ใช่ศูนย์ทั้งหมดแม้ว่าสิ่งนี้จะนำไปสู่ฟังก์ชันที่มีหลายค่าก็ตาม: ดูลอการิทึมเชิงซ้อนสำหรับข้อมูลเพิ่มเติม

ฟังก์ชันลอการิทึมธรรมชาติถ้าถือว่าเป็นฟังก์ชันที่มีมูลค่าจริงของตัวแปรจริงคือฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียลซึ่งนำไปสู่อัตลักษณ์:

ลอการิทึมสามารถกำหนดฐานบวกใด ๆ อื่น ๆ กว่า 1, ไม่เพียง แต่อี อย่างไรก็ตามลอการิทึมในฐานอื่นแตกต่างกันเพียงแค่ตัวคูณคงที่จากลอการิทึมธรรมชาติและสามารถกำหนดได้ในรูปแบบหลัง ยกตัวอย่างเช่นฐาน-2 ลอการิทึม (เรียกว่าลอการิทึมไบนารี ) เท่ากับลอการิทึมธรรมชาติหารด้วยLN 2ที่ลอการิทึมธรรมชาติของ 2

ลอการิทึมมีประโยชน์สำหรับการแก้สมการที่สิ่งที่ไม่รู้จักปรากฏเป็นเลขชี้กำลังของปริมาณอื่น ๆ ตัวอย่างเช่นลอการิทึมใช้เพื่อแก้ปัญหาครึ่งชีวิตค่าคงที่การสลายตัวหรือเวลาที่ไม่รู้จักในปัญหาการสลายตัวแบบเอ็กซ์โปเนนเชียล พวกเขามีความสำคัญในหลายสาขาวิชาคณิตศาสตร์และสาขาวิชาทางวิทยาศาสตร์และมีการใช้ในทางการเงินในการแก้ปัญหาที่เกี่ยวข้องกับดอกเบี้ยทบต้น