คณิตศาสตร์เรื่อง ภาคตัดกรวย พาราโบลา
พาราโบลา
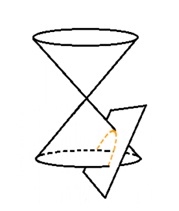
กราฟพาราโบลาอาจวางตัวได้หลายแบบ ตอนนี้เราจะพิจารณาการวางตัวของกราฟ
เพียง 2 ลักษณะคือ วางตัวตามแนวแกน x (กราฟตะแคงขวา, ซ้าย) และตามแนวแกน y (กราฟหงาย, คว่ำ)
1) พาราโบลาที่มีแกนวางตัวในทิศของแกน y (กราฟหงาย, คว่ำ)
พิจารณารูปต่อไปนี้
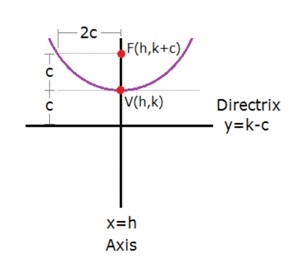
จากรูปจะได้ว่า
– สมการพาราโบลาที่มีจุดยอดที่ V(h, k) คือ
ดังนั้นถ้าจุดยอดอยู่ตรงจุดกำเนิดจะได้สมการเป็น
– ระยะห่างระหว่างจุดยอดไปถึงจุดโฟกัส (F) เท่ากับ c (พิกัดของ F ในรูปนี้จึงเป็น F(h, k+c))
ซึ่งระยะทางนี้จะเท่ากับระยะห่างระหว่างจุดยอดกับเส้นไดเร็คทริกซ์
– เลตัสเรกตัม (Latus rectum) หรือเส้นที่แสดงความกว้างของพาราโบลา ณ จุดโฟกัส มีความยาวเท่ากับ |4c|
– สำหรับค่า c ถ้าเป็นบวกกราฟจะหงายขึ้น ถ้าเป็นลบกราฟจะคว่ำลง
– กราฟวางตัวไปในแนวของตัวแปรที่มีกำลังเป็นหนึ่ง ในกรณีคือ y ดังนั้นจึงได้กราฟในทิศทางของแกน y
2) พาราโบลาที่มีแกนวางตัวในทิศของแกน x (กราฟตะแคงขวา, ซ้าย)
ลองมาดูอีกรูปหนึ่งครับ
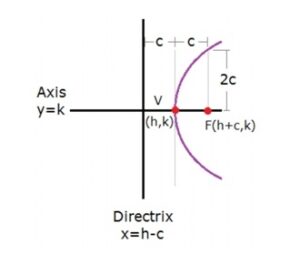
จากรูปนี้ จะได้ว่า
– สมการพาราโบลาที่มีจุดยอดอยู่ที่ V(h, k) คือ
ดังนั้นถ้าจุดยอดอยู่ที่จุดกำเนิด จะได้สมการเป็น
– ระยะห่างระหว่างจุดยอดไปถึงจุดโฟกัส (F) เท่ากับ c ดังนั้นเราจึงสามารถหาพิกัดของ F ในรูปนี้ได้เป็น
F(h+c, k)
– เลตัสเรกตัม มีความยาวเท่ากับ |4c|
– สำหรับค่า c ถ้าเป็นบวกกราฟจะตะแคงขวา ถ้าเป็นลบกราฟจะตะแคงซ้าย
– ในกรณีนี้ สมการพาราโบลามีตัวแปร x กำลังเป็นหนึ่ง ดังนั้นจึงได้กราฟวางตัวในทิศทางของแกน x
รูปแบบของพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)
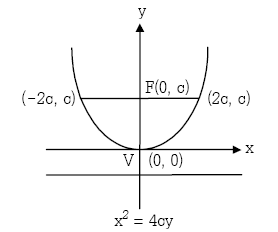
พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน y
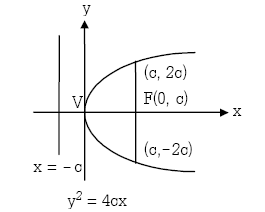
พาราโบลาซึ่งมีจุดยอดที่จุด (0,0) และแกนของรูปทับแกน x
เราสามารถสรุปสมการพาราโบลาออกมาได้ดังนี้









