ความหมายของศัพท์ตรรกศาสตร์
คำว่า “ตรรกศาสตร์” ได้มาจากศัพท์ภาษาสันสฤตสองศัพท์ คือ ตรฺรก และศาสตฺร ตรรก หมายถึง การตรึกตรอง ความคิด ความนึกคิด และคำว่า ศาสตฺร หมายถึง วิชา ตำรา รวมกันเข้าเป็น “ตรรกศาสตร์” หมายถึง วิชาว่าด้วยความนึกคิดอย่างเป็นระบบ ปราชญ์ทั่วไปจึงมีความเห็นร่วมกันว่า ตรรกศาสตร์ คือ วิชาว่าด้วย การใช้กฎเกณฑ์ การใช้เหตุผล วิชาตรรกศาสตร์นั้นมีนักปราชญ์ทางตรรกศาสตร์ได้นิยามความหมายไว้มากมาย นักปราชญ์เหล่านั้น คือ
1.พจนานุกรมศัพท์ปรัชญาอังกฤษ – ไทย ฉบับราชบัณฑิตยสถาน นิยามความหมายว่า “ตรรกศาสตร์ คือ ปรัชญาสาขาที่ว่าด้วยการวิเคราะห์และตัดสินความสมเหตุสมผลในการอ้างเหตุผล”
2.กีรติ บุญเจือ นิยามความหมายว่า “ตรรกวิทยา คือ วิชาที่ว่าด้วยกฎเกณฑ์การใช้เหตุผล”
3.”Wilfrid Hodges” นิยามความหมายว่า “ตรรกศาสตร์ คือ การศึกษาระบบข้อเท็จจริงให้ตรงกับความเชื่อ”
ประพจน์หมายถึง ประโยคหรือข้อความที่ใช้สำหรับบอกค่าเป็นจริงหรือเป็นเท็จเพียงอย่างใดอย่างหนึ่ง ส่วนประโยคที่ไม่สามารถบอกกค่าความจริงหรือเป็นเท็จได้จะไม่เรียกว่าประพจน์ตัวอย่างประโยคหรือข้อความที่เป็นประพจน์ เช่นØ ดวงอาทิตย์ขึ้นทางทิศตะวันออกØ สุนัขมี 4 ขาØ เดือนมกราคมมี 30 วัน ตัวอย่างประโยคหรือข้อความที่ไม่เป็นประพจน์ เช่นØ ห้ามเดินลัดสนามØ เธอกำลังจะไปหนØ Y + 5 = 8
ประโยคเปิดคือ ประโยคหรือข้อความที่ทีค่าตัวแปรอยู่ในประโยค และยังไม่สามารถทราบค่าความจริง ถ้าทำการแทนค่าตัวแปรนั้นด้วยค่าบางอย่าง จะทำให้ประโยคหรือข้อความนั้นมีค่าออกมาเป็นจริงหรือเป็นเท็จ ตัวอย่าง เช่นØ เขาเป็นนักฟุตบอลทีมชาติไทย ถ้าแทนเขาด้วยชื่อของนักฟุตบอลทีมชาติไทย ประโยคนี่จะมีค่าเป็นจริง ถ้าแทนเขาด้วยชื่ออื่นที่ไม่ใช่ชื่อของนักฟุตบอลทีมชาติไทย ประโยคนี้จะมีค่าเป็นเท็จØ Y + 5 = 8 ถ้าแทนค่าของ Y ด้วย 3 ประโยคนี้จะมีค่าออกมาเป็นจริง ถ้า
แทนค่าของ Y ด้วยตัวเลขอื่น ประโยคนี้จะมีค่าออกมาเป็นเท็จ
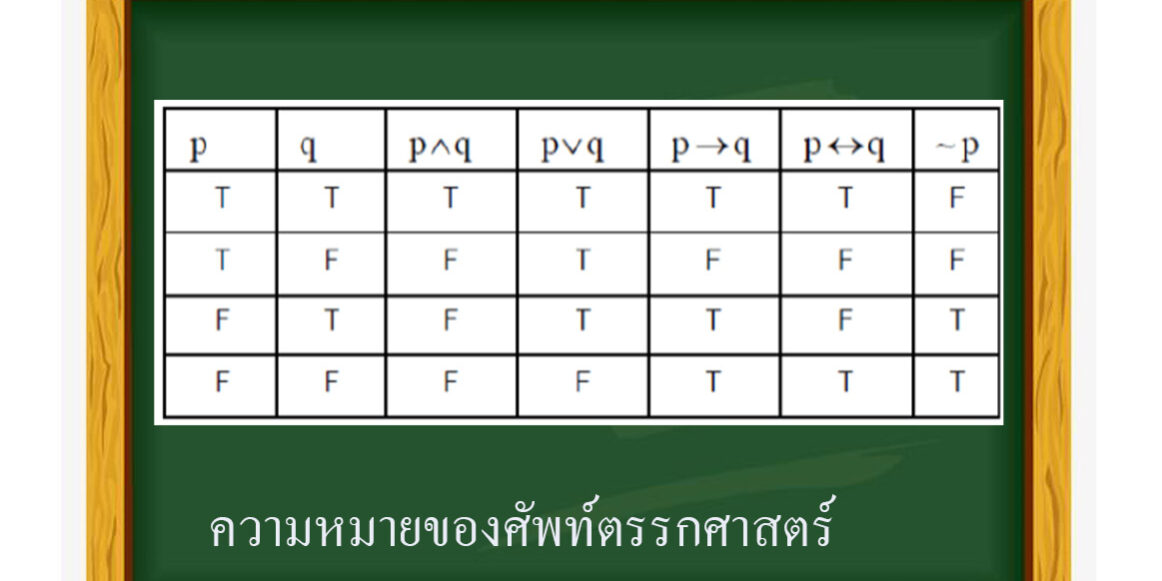
ตัวเชื่อมทางตรรกศาสตร์ตัวเชื่อมทางตรรกศาสตร์ใช้สำหรับกรณีที่ต้องการเชื่อมประพจน์มากกว่า 1 ประพจน์เข้าด้วยกัน เรียกว่า ประพจน์เชิงประกอบ ส่วนประพจน์ที่ไม่มีตัวเชื่อมทางตรรกศาสตร์ เรียกว่าประพจน์เดี่ยว สัญลักษณ์ที่ใช้เป็นตัวเชื่อมทางตรรกศาสตร์มีดังนี้ตัวเชื่อทางตรรกศาสตร์ สัญลักษณ์
และ ∧
หรือ ⋁
ถ้า…แล้ว →
ก็ต่อเมื่อ
ไม่ ~
ค่าความจริงของประพจน์เชิงประกอบผลลัพธ์ที่ได้ประพจน์เชิงประกอบที่ใช้ตัวเชื่อมทางตรรกศาสตร์แต่ละชนิด จะมีผลลัพธ์ที่ต่างกันออกไป ประพจน์ที่ประกอบด้วยหลายตัวเชื่อทางตรรกศาสตร์
การหาความจริงของประพจน์ที่ประกอบด้วยหลายตัวเชื่อมทางตรรกศาสตร์ สามารถทำได้โดยใช้ตารางค่าความจริง การบอกลำดับของการกระทำระหว่างประพจน์จะใช้วงเล็บในการบอกลำดับการทำงาน ถ้ามีนิเสธ ให้ทำในส่วนของนิเสธของประพจน์เป็นอันดับแรก ตัวอย่างของการหาค่าความจริงของประพจน์ที่ประกอบด้วยหลายตัวเชื่อมทางตรรกศาสตร์
ตัวอย่างที่ 1 จงเขียนตารางค่าความจริงของ ~Q^R
จากตัวอย่างประพจน์นี้ปรกอบด้วย 2 ประพจน์ย่อย ดังนี้ ค่าความจริงที่สามารถเป็นไปได้มีทั้งหมด 4 กรณี สามารถเขียนเป็นตารางค่าความจริงได้ ดังนี้Q R ~Q ~Q^R
F F T F
F T T T
T F F F
T T F F
ตัวอย่างที่ 2 จงเขียนตารางค่าความจริงของ (~Q^R) v (R^~S)
จากตัวอย่างประพจน์นี้ปรกอบด้วย 3 ประพจน์ย่อย คือ Q,R และ S ดังนั้นค่าความจริงที่สามารถเป็นไปได้มีทั้งหมด 23 = 8 กรณี สามารถเขียนเป็นตารางความจริงได้ ดังนี้
Q R S ~R Q^~S ~S R^~S (A^~R) v (R^~S)
F F F T F T F F
F F T T F F F F
F T F F F T T T
F T T F F F F F
T F F T T T F T
T F T T T F F T
T T F F F T T T
T T T F F F F F
ตัวอย่างที่ 3 จงเขียนตารางค่าความจริงของ (~Q^R)(Q^R)
จากตัวอย่างประพจน์นี้ปรกอบด้วย 2 ประพจน์ย่อย ดังนี้ ค่าความจริงที่สามารถเป็นไปได้มีทั้งหมด 4 กรณี สามารถเขียนเป็นตารางค่าความจริงได้ ดังนี้
Q R ~Q ~Q v R Q^R (~QvR)(Q^R)
F F T T F F
F T T T F F
T F F F F T
T T F T T T
เชิงประกอบที่ประกอบด้วยประพจน์ย่อย 2 ประพจน์ กรณีที่สามารถเป็นไปได้ คือ 4 กรณี โดยที่ทุกกรณีจะให้ค่าความจริงออกมาเป็นจริงทั้งหมด
ตัวอย่างที่ 1 จงทำการตรวจสอบว่าประพจน์ P–>(QvP) เป็นสัจนิรันดร์หรือไม่
Q P QvP P–>(QvP)
F F F T
F T T T
T F T T
T T T T
ประพจน์ P –>(QvP) เป็นสัจนิรันดร์
ตัวอย่างที่ 2 จงทำการตรวจสอบว่าประพจน์ (P–>(QvR))v(Q(P^R)) เป็นสัจนิรันดร์หรือไม่
P Q R QvR P–>(QvR) P^R (Q(P^R) (P–>(QvR))v(Q(P^R))
F F F F T F T T
F F T T T F T T
F T F T T F F T
F T T T T F F T
T F T F F F T T
T F F T T T F T
T T T T T F F T
T T T T T T T T
ประพจน์ (P–>(QvR))v(Q(P^R)) เป็นสัจนิรันดร์
ประพจน์ที่สมมูลกัลป์ ประพจน์สองประพจน์มีความสมมูลกัน ก็ต่อเมื่อประพจน์ทั้งสองประกอบด้วยประพจน์ย่อยที่เหมือนกันและให้ค่าความ จริงออกมาเหมือนกันในทุกกรณี ใช้สัญลักษณ์ แทนการสมมูลกัน
ตัวอย่างที่ 1 จงทำการตรวจสอบว่าประพจน์ P–>Q และ ~Q–>~P เป็นประพจน์ที่สมมูลกันหรือไม่
P Q P–>Q ~P ~Q ~Q–>~P
F F T T T T
F T T T F T
T F F F T F
T T T F F T
P–>Q และ ~Q–>~P เป็นประพจน์ที่สมมูลกัน
หรือเขียนได้ว่า P–>Q ~Q–>~P
ตัวอย่างที่ 2 จงทำการตรวจสอบว่าประพจน ์(P–>(QvR))v(Q(P^R)) เป็นสัจนิรันดร์หรือไม่
P Q P–>Q ~(P–>Q) ~Q P^~Q
F F T F T F
F T T F F F
T F F T T T
T T T F F F
ประพจน์ ~(P–>Q) และ P^~Q เป็นประพจน์ที่สมมูลกัน
หรือเขียนได้ว่า ~(P–>Q) P^~Q
ตรรกศาสตร์เบื้องต้น
1. ประพจน์ (Propostion) คือ ตรรกศาสตร์เป็นวิชาหนึ่งที่เกี่ยวข้องกับชีวิตประจำวันของเรา เป็นอย่างมาก เพราะว่าใน สภาพ สังคมทุกวันนี้ต้องมีการติดต่อสื่อสารอยู่ตลอดเวลา ไม่ว่าจะอยู่ในลักษณะการพูดหรือการเขียน ข้อ ความ ทั้งนี้เพื่อที่จะให้อีกฝ่ายหนึ่งได้เข้าใจรับรู้และในบางครั้งก็ต้องมีการตัดสินใจ รับรู้ และใน บาง ครั้งก็ต้องมีการตัดสินใจซึ่งการรับรู้และการตัดสินใจจะเกิดขึ้นได้นั้นผู้ที่รับฟังหรืออ่านข้อความ นั้น ต้อง รู้ว่าข้อความที่พูดหรือเขียนนั้นเป็นจริงหรือเท็จ ในการพิจารณาว่าคำพูดหรือข้อความใดเป็นจริงหรือเท็จนั้น จะเกี่ยวข้องกับ วิชา ตรรกศาสตร์ควรจะศึกษาว่าคำพูดนั้นเป็นจริงหรือเท็จ เช่น
1. จังหวัดเชียงใหม่อยู่เหนือจังหวัดนครสวรรค์ เราบอกได้ว่าข้อความนี้เป็นจริง
2. พระอาทิตย์ขึ้นทางทิศตะวันตก เราบอกได้ว่าข้อความนี้เป็นเท็จ
3. โปรดให้เงินผมบ้าง เราไม่สามารถบอกได้ว่าข้อความนี้เป็นจริงหรือเท็จ
ดังนั้นข้อความนี้จึงไม่ใช่ ประพจน์
บทนิยามประพจน์ คือ ประโยคที่มีค่าความจริงหรือเท็จอย่างใดอย่างหนึ่งเพียง อย่าง เดียว ซึ่งประโยคดังกล่าวอาจจะอยู่ในประโยคบอกเล่า หรือในประโยคปฏิเสธก็ได้
ตัวอย่างประโยคที่ไม่เป็นประพจน์
1. ประโยคคำถาม เช่น ใครกันนะ
2. ประโยคคำสั่ง เช่น จงนั่งลง
3. ประโยคขอร้อง เช่นช่วยปิดหน้าต่างให้ หน่อย
4. ประโยคอ้อนวอน เช่น โปรดเมตตาด้วยเถิด
5. ประโยคแสดงความ ปรารถนาเช่น ฉันอยากเป็นนก
6. ประโยคอุทาน เช่น อุ๊ย….เจ็บ
7. สุภาษิตคำพังเพย เช่น น้ำลดตอพุด
8. ประโยคเปิด เช่น เขาเป็นดารานักร้อง
การแทนประพจน์จะใช้สัญลักษณ์ p, q, r … เพื่อแทนประพจน์ที่แตกต่างกัน ข้อความที่มีกริยาเพียงตัวเดียวและเป็นประพจน์จะเรียกว่าประพจน์เบื้องต้น
2. ประโยคเปิด (Open Sentence)
ประโยคเปิด คือ ประโยคบอกเล่าหรือประโยคปฏิเสธที่มีตัวแปร ไม่เป็นประพจน์ และเมื่อแทนที่ตัวแปรด้วยสมาชิกในเอกภพสัมพัทธ์แล้วได้ประพจน์
ประโยคเปิด เช่น
1.เขาเป็นนักว่ายน้ำทีมชาติไทยเขาเป็นนักฟุตบอลทีมชาติไทย ถ้าแทนเขาด้วยชื่อของนักฟุตบอลทีมชาติไทยประโยคนี้จะมีค่าเป็นจริง ถ้าแทนเข้าด้วยอื่นที่ไม่ใช่ชื่อนักฟุตบอลทีมชาติไทย ประโยคนี้จะมีค่าเป็นเท็จ
2. x – 6 = 10 Y + 5 = 8 ถ้าแทนค่าของ Y ด้วย 3 ประโยคนี้จะมีค่าออกมาเป็นจริง ถ้าแทนค่าของ Y ด้วยตัวเลขอื่น ประโยคนี้จะมีค่าออกมาเป็นเท็จ
ประโยคที่ไม่ใช่ประโยคเปิด เช่น
1. 10 เป็นคำตอบของสมการ x – 1 = 7
2. โลกหมุนรอบตัวเอง
3. จงหาค่า x จากสมการ 2x + 1 = 8
4. กรุณานั่งเงียบ ๆ
5. ห้ามสูบบุหรี่
ขอบคุณข้อมูล อ้างอิง : http://www.thaigoodview.com