ฟังก์ชันพหุนาม (polynomial function)
พหุนาม คือนิพจน์ที่สร้างจากตัวแปรอย่างน้อยหนึ่งตัวและค่าคงที่ โดยใช้การดำเนินการแค่ การบวก การลบ และการคูณ
ตัวอย่าง
เช่น นิพจน์ y(2xz3 − 4)x − 2 + (0.9x + z)y เป็นพหุนาม (เนื่องจาก z3 เป็นการเขียนย่อจาก z\cdot z\cdot z) แต่นิพจน์ {1 \over x^2 + 1} ไม่ใช่พหุนาม เนื่องจากมีการหาร เช่นเดียวกับ นิพจน์ (5 + y)x เนื่องจากไม่สามารถเขียนให้อยู่ในรูปของการคูณกันที่ไม่ขึ้นกับค่าของตัวแปร x ได้ นอกจากนี้ ยังมีการนิยาม พหุนาม ในรูปแบบจำกัด กล่าวคือ พหุนามคือ นิพจน์ที่เป็นผลรวมของผลคูณระหว่างตัวแปรกับค่าคงที่ ยกตัวอย่างเช่น 2x2yz3 − 3.1xy + yz − 2 อย่างไรก็ตาม ข้อจำกัดนี้เป็นเพียงข้อจำกัดที่ผิวเผิน เนื่องจากสามารถใช้กฎการ แจกแจงแปลง พหุนามภายใต้นิยามแรกให้เป็นพหุนามภายใต้นิยามที่สองได้ ในการใช้งานทั่วไปมักไม่แยกแยะความแตกต่างทั้งสอง นอกจากนี้ในบริบททั่วไปมักนิยมถือว่าโดยทั่วไปพหุ นามจะอยู่ในรูปแบบจำกัดนี้ แต่เมื่อต้องการแสดงว่าอะไรเป็นพหุนาม มักใช้รูปแบบแรกเนื่องจากสะดวกมากกว่า
ฟังก์ชันพหุนาม คือ ฟังก์ชันที่นิยามด้วยพหุนาม ตัวอย่างเช่น ฟังก์ชัน f นิยามด้วย f(x) = x3−x เป็นฟังก์ชันพหุนาม ฟังก์ชันพหุนามเป็นฟังก์ชันเรียบประเภท หนึ่งที่สำคัญ โดยคำว่า
เรียบในที่นี้หมายความว่าสามารถหาอนุพันธ์ได้อย่างไม่มีที่สิ้นสุด นั่นคือ เป็นฟังก์ชันที่มีอนุพันธ์ทุก ๆ อันดับที่จำกัด
ฟังก์ชันที่ควรรู้จัก
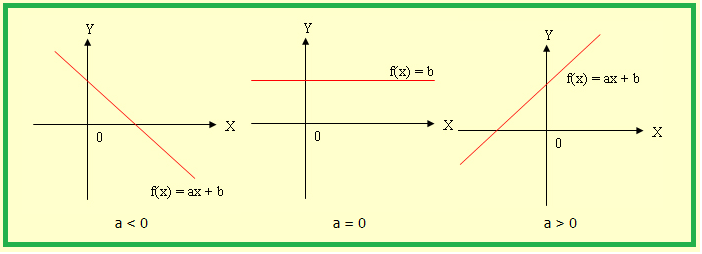
ฟังก์ชันเชิงเส้น (linear function)
f(x) = ax + b เมื่อ a และ b เป็นจำนวนจริง
กราฟของฟังก์ชันเชิงเส้นจะมีลักษณะเป็นเส้นตรง
ฟังก์ชันขั้นบันได (step function)
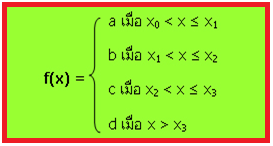
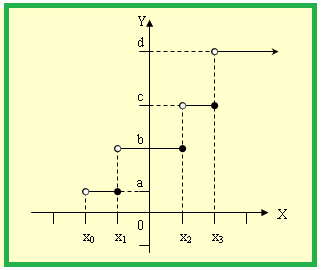
กราฟของฟังก์ชันนี้จะมีรูปร่างคล้ายขั้นบันได
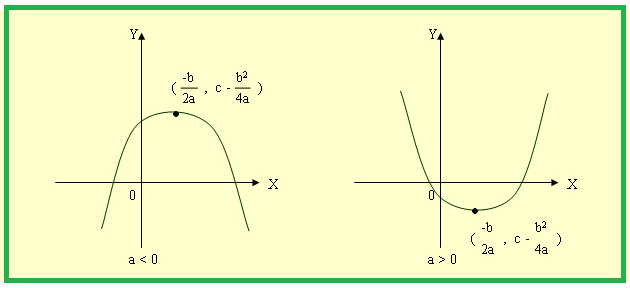
ฟังก์ชันกำลังสอง (quadratic function)
f(x) = ax2 + bx + c เมื่อ a และ b เป็นจำนวนจริง
กราฟของฟังก์ชันกำลังสองจะมีลักษณะเป็นรูปพาราโบลา

ฟังก์ชันพหุนาม (polynomial function)

ฟังก์ชันตรรกยะ (rational function)

ฟังก์ชันที่เป็นคาบ (periodic function)
f เป็นฟังก์ชันที่เป็นคาบ ก็ต่อเมื่อ มีำจำนวนจริง p ที่ทำให้ f(x+p) = f(x) สำหรับ ทุกค่าของ x และ x+p ที่อยู่ในโดเมนของ f






