ภาคตัดกรวย (Conic Section)-เรื่องวงกลม
ความชันของเส้นตรง (Slope : m)
คือ อัตราส่วนระหว่างค่า y ที่เปลี่ยนแปลงไป ต่อค่า x ที่เปลี่ยนแปลงไป ใช้ สัญลักษณ์ m โดยค่า m อาจะเป็นบวก หรือลบ หรือเป็นศูนย์ก็ได้
- ถ้า m>0 แสดงว่า เส้นตรงนี้เฉียงขึ้นทางขวา
- ถ้า m<0 แสดงว่า เส้นตรงนี้เฉียงลงทางขวา
- ถ้า m=0 แสดงว่า เป็นเส้นนอนขนานแกน x
- ส่วนเส้นตั้งขนานกับแกน y นั้น m หาค่าไม่ได้ (เป็นอนันต์)
เส้นขนานและเส้นตั้งฉาก
- เส้นตรงที่ไม่ขนานกับแกน y จะขนานกันก็ต่อเมื่อมีความชันเท่ากัน
- เส้นตรงที่ขนานกับแกน y จะขนานกับเส้นตรงที่ขนานกับแกน y เส้นอื่น ๆ ด้วย
- เส้นตรงที่ไม่ขนานกับแกน y จะตั้งฉากกันก็ต่อเมื่อมีความชันคูณกันได้เท่ากับ -1
- เส้นตรงที่ขนานกับแกน y จะตั้งฉากกับเส้นตรงที่ขนานแกน x
วงกลม
นิยาม คือ เซตของคู่อันดับที่อยู่ห่างจากจุดคงที่จุดหนึ่ง เป็นระยะเท่ากัน” เรียกจุดคงที่นั้นว่า จุดศูนย์กลาง (Center; C) และเรียกระยะทางนั้นว่า รัศมี (Radius; r) ดังรูป
สมการวงกลม
- ที่มีจุดศูนย์กลางอยู่ที่จุด (h, k) และมีรัศมียาว r หน่วย จะมีสมการ คือ (x – h)2+ (y – k)2 = r2
- สมการรูปทั่วไป x2+y2+Dx+Ey+F=0
เส้นสัมผัสวงกลม คือ เส้นตรงที่ลากผ่านจุดบนวงกลมเพียงจุดเดียวเท่านั้น โดยเรียกจุด ๆ นี้ว่า จุดสัมผัส มีสมบัติทางเรขาคณิตอย่างหนึ่งของรูปวงกลมที่กล่าวว่า เส้นสัมผัสวงกลมจะตั้งฉากกับรัศมี ณ จุด สัมผัสนั้นเสมอ
วงกลม คือ เซตของจุดทุกบนระนาบ ซึ!งอยู่ห่างจากจุดคงที!จุดหนึ!งเป็ นระยะทางคงที!เสมอ
จุดคงที่ เรียกว่า จุดศูนย์กลางของวงกลม (center)
ระยะทางคงที เรียกว่า รัศมีของวงกลม (radius)
ในทางคณิตศาสตร์ ถือว่าวงกลมเป็ นเส้นโค้งทีสมบูรณ์ เครืองใช้ต่างๆ ของเรามักมีลักษณะเป็ นวงกลม เช่น ขันตักนำหน้าปัดนาฬิกา จานข้าว ถาด กระโถน เงินเหรียญ ท่านลองตรวจดูของใช้รอบกาย และทัวๆ ไป จะเห็น
ว่าการใช้ของทีมีลักษณะเป็นวงกลมนั นให้ความสะดวกมากที่ สุด ลองนึกดูว่าถ้า ล้อจักรยานยนต์ ล้อรถยนต์ ไม่มีลักษณะเป็นวงกลมแล้ว การเคลื่อนที่จะลําบากสักเพียงใด


วงรี
นิยาม : ให้ F1 และ F2 เป็นจุดใด ๆ จุด P ใด ๆ บนวงรีจะมีผลบวกของระยะจากจุดนั้นไปยังจุด F1 และ F2 เป็นค่าคงที่ค่าหนึ่งเสมอ โดยที่ค่าคงที่นี้มีค่ามากกว่าระยะ F1F2 หรือก็คือ F1P + F2P = k โดยที่ k > F1F2 สำหรับทุกจุด P บนวงรี เรียกจุด F1 และ F2 ว่า จุดโฟกัส และเรียก k ว่า ผลบวกคงตัว
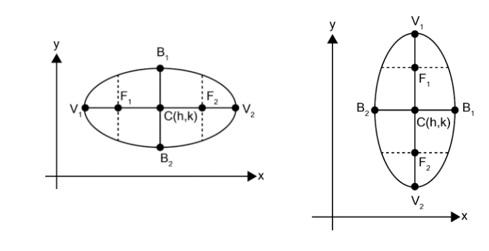
จากรูป เราจะเห็นส่วนประกอบของวงรี ดังนี้
การสร้างวงรีอาจพิจารณาได้ว่าคล้ายกับการวาดวงกลมนั่นเอง แต่เราจะทำการลดหรือขยายขนาดให้วงกลมกลายร่างเป็นวงรี
โดยการเพิ่มตัวคูณที่เทอม x2 หรือ y2 ซึ่งการสเกลแบบนี้ทำให้เรากำหนดได้ว่า วงรีจะอ้วน จะรีแค่ไหน หรือวางตัวในทิศของแกนใดเป็นหลัก
เราอาจแบ่งวงรีออกเป็น 2 แบบ ตามลักษณะการวางตัวตามแนวแกน x และแกน y ดังนี้ 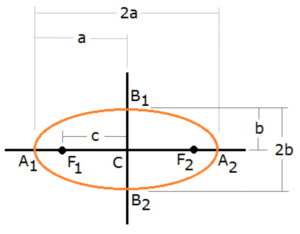
แกนที่แบ่งครึ่งรูปวงรี ได้แก่ แกนเอก (ยาว=2a) ซึ่งแสดงความยาวของวงรี
ส่วนอีกแกนเรียกว่า แกนโท (ยาว=2b) แสดงถึงความกว้างของวงรี ซึ่ง a>b เสมอ
จากรูปข้างบน ถ้าจุดกำเนิดอยู่ที่ C(h, k) จะได้พิกัดของจุดปลายแกนทั้ง 4 จุด ดังนี้
พิกัดของจุดปลายแกนเอก A1 คือ (h-a, k)
พิกัดของจุดปลายแกนเอก A2 คือ (h+a, k)
พิกัดของจุดปลายแกนโท B1 คือ (h, k+b)
พิกัดของจุดปลายแกนโท B2 คือ (h, k-b)
ข้อสังเกตวงรี:
1. สมการวงรีจะคล้ายกับวงกลม วิธีสังเกตว่าสมการนี้ใช่วงรีหรือไม่ ให้สังเกตโดย
– จัดรูปให้เป็น x2 และ y2 สัมประสิทธิ์หน้าทั้งสองเทอมนี้เป็นค่าบวกแต่มีค่าไม่เท่ากัน
(ตัวส่วนไม่เท่ากัน ซึ่งเป็นการขยายระยะแกนเอกและแกนโท)
– ด้านขวาของสมการเป็น 1
2. วงรีวางตัวแบบไหน ให้ดูจากแกนเอก แกนโท เพราะแกนเอกยาวกว่าแกนโทเสมอ นั่นคือ a>b เสมอ
สำหรับตัวส่วน a, b จะเป็นความยาวครึ่งหนึ่งของแกนเอก และแกนโทตามลำดับ
– ถ้า a อยู่กับ x และ b อยู่กับ y แสดงว่าแกนเอกของวงรีวางนอนขนานไปกับแกน x เหมือนในรูปตัวอย่างข้างบน
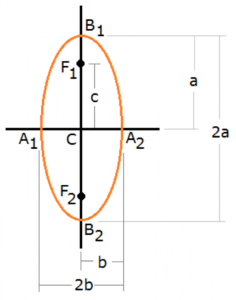
– ถ้า a อยู่กับ y และ b อยู่กับ x แสดงว่าแกนเอกของวงรีวางตั้งขึ้นขนานไปกับแกน y ดังรูปในตัวอย่างข้างล่างนี้
2) วงรีที่วางตัวในแนวแกน y (แนวตั้ง)
สมการวงรี:
ระยะโฟกัส (F):
จากรูป ถ้าจุดกำเนิดอยู่ที่ C(h, k) จะได้พิกัดของจุดปลายแกนทั้ง 4 จุด ดังนี้
พิกัดของจุดปลายแกนเอก B1 คือ (h, k+a)
พิกัดของจุดปลายแกนเอก B2 คือ (h, k-a)
พิกัดของจุดปลายแกนโท A1 คือ (h-b, k)
พิกัดของจุดปลายแกนโท A2 คือ (h+b, k)




สรุป
1. จุดศูนย์กลางวงรี (จุด C(h, k)) คือ จุดกึ่งกลางระหว่างจุดโฟกัสทั้งสองจุด กำหนดให้จุดโฟกัสทั้งสองห่างจากจุดศูนย์กลาง c หน่วย จะได้ว่า จุดโฟกัสทั้งสองห่างกัน 2c หน่วย โดย
- ถ้าวงรีเป็นแนวนอน จะได้ว่าจุดโฟกัสคือ (h ± c, k)
- ถ้าวงรีเป็นแนวตั้ง จะได้ว่าจุดโฟกัสคือ (h, k ± c)
2. แกนเอก (จากรูปคือเส้นตรง V1, V2) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี และลากผ่านจุดโฟกัสทั้งสองจุด กำหนดให้ แกนเอกยาว 2a หน่วย
3.จุดยอดของวงรี(จากรูปคือจุด V1 และ V2) คือ จุดปลายของแกนเอก จะเห็นว่า ผลบวกคงตัว จะมีค่าเท่ากับความยาวแกนเอก = 2a หน่วย โดย
- ถ้าวงรีเป็นแนวนอน จะได้ว่าจุดยอดคือ (h ± a, k)
- ถ้าวงรีเป็นแนวตั้ง จะได้ว่าจุดยอดคือ (h, k ± a)
- จุดกึ่งกลางระหว่างจุดยอดทั้งสองจุด คือ จุดศูนย์กลางวงรี
4.แกนโท(เส้นตรง B1B2) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี โดยตั้งฉากกับแกนเอก และผ่านจุดศูนย์กลางวงรี กำหนดให้ แกนโทยาว 2b หน่วย ดังนั้น จุดกึ่งกลางระหว่างจุดปลายของแกนโท คือ จุดศูนย์กลางวงรี
5. เส้นเลตัสเรกตัม (Latus Rectum) คือ เส้นประทั้งสองเส้นในรูปวงรีแนวนอนและวงรีแนวตั้ง ซึ่งเส้น Latus Rectum คือ ส่วนของเส้นตรงที่มีจุดปลาย อยู่บนวงรี (คอร์ดของวงรี) โดยตั้งฉากกับแกนเอกและผ่านจุดโฟกัส
6. ค่าความเยื้องศูนย์กลางของวงรี (e) คือ ค่าที่บอกความรีของวงรี โดย e = c/a โดย
- ค่า e มีค่าอยู่ในช่วง (0, 1)
- หาก e มีค่าเข้าใกล้ 1 วงรีจะรีมาก
- หาก e มีค่าเข้าใกล้ 0 วงรีจะรีน้อย






