การศึกษาภาคตัดกรวยวิธีทางเรขาคณิตวิเคราะห์ (analytic geometry]
การศึกษาภาคตัดกรวยสามารถศึกษาได้หลายแนวทาง ในที่นี้จะศึกษาภาคตัดกรวยโดยใช้วิธีทางเรขาคณิตวิเคราะห์
รูปที่ 1: การศึกษาภาคตัดกรวย
กรวยเป็นรูปเรขาคณิตที่มีวิธีการสร้างในเชิงคณิตศาสตร์ ดังนี้
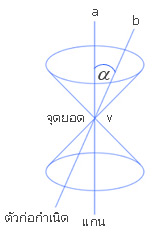
ให้ a และ b เป็นเส้นตรงใดๆ สองเส้นตัดกันที่จุด V เป็นมุมแหลม ให้เส้นตรง a และจุด V ตรึงอยู่กับที่ ผิวที่เกิดจากการหมุนเส้นตรง b รอบเส้นตรง a (โดยมุม ระหว่างเส้นตรง a และ b มีขนาดคงตัว) เรียกว่า กรวยกลมตรง (right circular cone) ดังแสดงในรูปที่ 1 ในที่นี้เราจะศึกษาเฉพาะกรวยกลมตรงเท่านั้นและจะเรียกสั้นๆ ว่า กรวย เส้นตรงที่ตรึงอยู่กับที่ เรียกว่า แกน (axis) ของกรวย จุด V เรียกว่า จุดยอด (vertex)
เส้นตรง b ที่ผ่านจุด V ทำมุม กับแกนของกรวย เรียกว่า ตัวก่อกำเนิด (generator) ของกรวย จุดยอด V แบ่งกรวยออกเป็นสองข้าง (nappes) ซึ่งอยู่คนละด้านของจุดยอด
ภาคตัดกรวย คือรูปในระนาบที่เกิดจากการตัดกันของระนาบกับกรวย ภาคตัดกรวยที่จะศึกษากันเกิดจากระนาบที่ไม่ผ่านจุดยอดของกรวยดังแสดงในรูปที่ 2 เมื่อระนาบตั้งฉากกับแกนของกรวย ระนาบตัดกรวยข้างเดียว ได้ภาคตัดกรวยที่เรียกว่า วงกลม (circle)
เมื่อระนาบไม่ตั้งฉากกับแกนของกรวยแต่ทำมุมแหลมกับแกนของกรวยขนาดใหญ่กว่า ระนาบจะตัดกรวยข้างเดียวได้ภาคตัดกรวยที่เรียกว่า วงรี (ellipse)
เมื่อระนาบขนานกับตัวก่อกำเนิดของกรวยระนาบจะตัดกรวยข้างเดียว ได้ภาคตัดกรวยที่เรียกว่าพาราโบลา (parabola)
และเมื่อระนาบขนานกับแกนของกรวย ระนาบจะตัดกรวยสองข้างได้ภาคตัดกรวยสองข้างได้ภาคตัดกรวยที่เรียกว่า ไฮเพอร์โบลา (hyperbola)
ถ้าระนาบผ่านจุดยอดของกรวย รอยตัดของระนาบกับกรวยจะเป็นจุด หรือเส้นตรงหนึ่งเส้น หรือเส้นตรงสองเส้นตัดกัน ซึ่งเรียกลักษณะดังกล่าวว่า ภาคตัดกรวยลดรูป (degenerate conics) ดังแสดงในรูปที่ 3
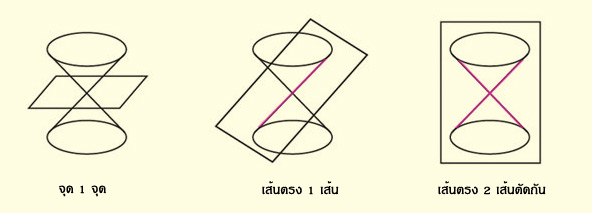
รูปที่ 3 ภาคตัดกรวยลดรูป
ศึกษาภาคตัดกรวยโดยใช้เรขาคณิตวิเคราะห์
ในการศึกษาภาคตัดกรวยโดยใช้เรขาคณิตวิเคราะห์ มีประเด็นหลักที่จะศึกษา 2 ประเด็น คือ
- หาสมการของภาคตัดกรวยแต่ละชนิด
- จำแนกหรือระบุว่ากราฟของสมการเป็นภาคตัดกรวยชนิดใด แล้วเขียนกราฟของสมการเมื่อกำหนดสมการรูปแบบทั่วไปของภาคตัดกรวย
