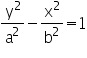ไฮเพอร์โบลา (Hyperbola) ม.4
การเลื่อนกราฟของสมการ
ถ้า h และ K เป็นจำนวนจริงบวกแล้ว การแทน x ด้วย x-h หรือ x+h และการแทน y ด้วย
y-k หรือ y+k จะมีผลต่อกราฟของสทการใดๆ ในตัวแปร x และ y ดังนี้
วิธีการแทน กราฟเลื่อนไปอย่างไร
1. แทน x ด้วย x-h ทางขวา h หน่วย
2. แทน x ด้วย x+h ทางซ้าย h หน่วย
3. แทน y ด้วย y-k ขึ้นบน k หน่วย
4. แทน y ด้วย y+k ลงล่าง k หน่วย
สรุป
นิยามของสมการไฮเพอร์โบลา
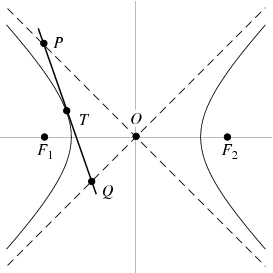
ไฮเพอร์โบลา (Hyperbola) คือเซตของจุดทั้งหมดในระนาบซึ่งผลต่างของระยะทางจากจุดใดๆไปยังจุด F1 และ F2 ที่ตรึงอยู่กับที่มีค่าคงตัว โดยค่าคงตัวน้อยกว่าระยะห่างระหว่างจุดคงที่ที่ตรึงอยู่กับที่ทั้งสอง จุด F1 และ F2 ดังกล่าวนี้เรียกว่า โฟกัส (Focus) ของไฮเพอร์โบลา
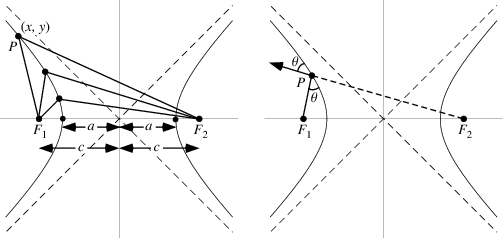
ให้ระยะทางจากจุด F1 และ F2 ไปยังเส้นกราฟมีค่าเท่ากับ r1=F1 และ r2=F2 และระยะทางระหว่างจุด F และจุด F2 มีค่าเท่ากับ 2c หรือเรียกอีกอย่างว่าค่า k ซึ่งค่า k นี้จะมีค่าเป็นบวกเสมอ
r2-r1 = k
ถ้าจุด P ซึ่งอยู่บนเส้นกราฟด้านซ้ายมืออยู่บนแกน x แล้ว
k = (c+a) – (c-a) = 2a
ดังนั้นเราสามารถคำนวณค่า k=2a ได้ หรือนั่นก็คือระยะทางระหว่างจุดยอดของกราฟไฮเพอร์โบลาทั้งสอง ข้อสังเกตุคือเส้นกราฟพาราโบลาที่เกิดจาดจุดโฟกัส F1 จะมีเส้นกราฟที่เกิดจาด F2 สะท้อนเหมือนกันอยู่ในฝั่งตรงข้ามเสมอ
สมการไฮเพอร์โบลา
รูปแบบของสมการไฮเพอร์โบลาจะแบ่งออกตามรูปกราฟสมการสองแบบ คือไฮเพอร์โบลาแบบตะแคง (ซ้ายขวา) และไฮเพอร์โบลาแบบตั้ง (บนล่าง) โดยทั้งสองรูปแบบมีสมการดังนี้
| ไฮเพอร์โบลาตะแคง | ไฮเพอร์โบลาตั้ง |
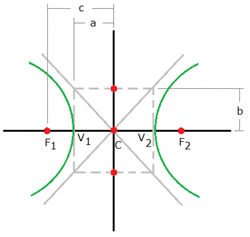
สมการไฮเพอร์โบลาคือ สังเกตว่าหน้า x เป็นบวก ดังนั้นแกนตามขวางจึงวางตัวในแนวแกน x (a อยู่กับ x)แกนตามขวาง (แกนที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเป็น 2a แกนสังยุค มีความยาวเป็น 2b ระยะโฟกัส มีความยาว
|
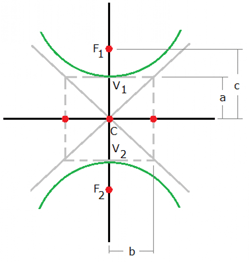
สมการไฮเพอร์โบลาคือ สังเกตว่าหน้า x เป็นบวก ดังนั้นแกนตามขวางจึงวางตัวในแนวแกน x (a อยู่กับ x)แกนตามขวาง (แกนที่ลากตัดกึ่งกลางของกราฟ) มีความยาวเป็น 2a แกนสังยุค มีความยาวเป็น 2b ระยะโฟกัส มีความยาว |
ข้อสังเกตุ: a ไม่จำเป็นต้องยาวกว่า b เหมือนในสมการวงรี แต่ถ้า a=b จะได้สี่เหลี่ยมจัตุรัสอยู่ตรงกลาง จะเรียกว่าเป็น ไฮเพอร์โบลามุมฉาก (Rectangular Hyperbola)

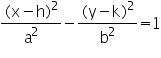 ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้
ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้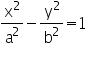
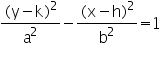 ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้
ถ้าจุดศูนย์กลางของสมการ c อยู่ที่จุด (0,0) เราจะได้สมการไฮเพอร์โบลาที่จุดกำเนิดดังนี้