สรุปสูตร สถิติ ทั้งหมด

1) ค่าเฉลี่ยเลขคณิต

2) มัธยฐาน

3) ฐานนิยม

4) ควอไทล์ เดไซล์ เปอร์เซนไทล์

5) การวัดการกระจาย

6) ความแปรปรวน และความแปรปรวนรวม

7) ค่ามาตรฐาน พื้นที่ใต้เส้นโค้งปกติ

9) ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล

การหาค่าเฉลี่ยเลขคณิตข้อมูลที่แจกแจงความถี่

วิธีการ หาค่าเฉลี่ย มัธยฐาน และฐานนิยม

การวัดแนวโน้มเข้าสู่ส่วนกลาง

ค่ากลาง คือ ค่าที่ใช้เป็นตัวแทนของข้อมูลชุดหนึ่ง ค่ากลางที่นิยมใช้มี 3 วิธีได้แก่

1) ฐานนิยม (Mode)

ฐานนิยม (Mode : Mo) หมายถึง ค่าของข้อมูลในชุดใดชุดหนึ่ง ซึ่งมีความถี่สูงที่สุดหรือซ้ำกันมากที่สุด การหาฐานนิยมแบ่งเป็น 2 กรณี

1.1) กรณีที่ข้อมูลไม่จัดเป็นกลุ่ม

Ex.

1.2) กรณีที่ข้อมูลจัดเป็นกลุ่ม

หาได้จากสูตร

Ex. จงหาฐานนิยมของข้อมูลต่อไปนี้

2) มัธยฐาน (Median)

มัธยฐาน (Median : Md) คือ ค่าที่อยู่ตรงกลางของชุดข้อมูลหลังจากทำการเรียงลำดับแล้ว มัธยฐานเป็นค่าที่แบ่งข้อมูลออกเป็นสองส่วน ส่วนหนึ่งมีค่าน้อยกว่าค่ามัธยฐาน อีกส่วนหนึ่งมีค่ามากกว่ามัธยฐาน การหามัธยฐานแบ่งเป็น 2 กรณี

2.1) กรณีที่ข้อมูลไม่แจกแจงความถี่

Ex. จงหามัธยฐานของข้อมูลต่อไปนี้

1) 45 20 30 55 40 50 60

2) 48 22 30 55 70 89 29 35

2.2) กรณีที่ข้อมูลแจกแจงความถี่

2.2.1) เรียงลำดับข้อมูลจากน้อยไปหามากโดยการหาความถี่สะสมจากน้อยไปมาก

2.2.2) หาตำแหน่งของมัธยฐานจาก n/2 เมื่อ n แทนจำนวนข้อมูลทั้งหมด

2.2.3) หาค่าของตำแหน่งที่คำนวณได้จากข้อ 2 โดยสูตร

L0 แทน ขอบเขตล่างของชั้นมัธยฐาน

I แทน ความกว้างของชั้นมัธยฐาน n แทน จำนวนข้อมูลทั้งหมด

F แทน ความถี่สะสมแบบน้อยกว่าจนถึงชั้นก่อนมัธยฐาน

f แทน ความถี่ของชั้นมัธยฐาน

หาความถี่สะสมแบบน้อยกว่าของข้อมูล

ตำแหน่งมัธยฐาน = n/2 = 40/2 = 20

ตำแหน่งที่ 20 มีคะแนนอยู่ในช่วง 40 – 49 ดังนั้นชั้น 40 – 49 เป็นชั้นมัธยฐาน

เปอร์เซนต์ไทล์ เดไซล์ ควอร์ไทล์

เปอร์เซนต์ไทล์ เดไซล์ ควอร์ไทล์ เป็นการวัดตำเเหน่งของข้อมูลชุดหนึ่งๆ เมื่อแบ่งคะแนนหรือข้อมูลทั้งหมดออกเป็น 100 ส่วน 10 ส่วน และ 4 ส่วน ตามลำลับ เพื่อใช้ในการเปรียบเทียบข้อมูล

เปอร์เซ็นไทล์ (Percentile Rank)

เปอร์เซ็นต์ไทล์ หมายถึงตำแหน่งที่แสดงให้ทราบว่ามีจำนวนร้อยละเท่าไหร่ของจำนวนคะแนนที่ค่าต่ำกว่าคะแนนที่ตำปหน่งนั้น เช่น นักศึกษาคนหนึ่งสอบวิชาสถิติได้คะแนน 54 คะแนน และคะแนน 54 นี้ อยู่ตำแหน่งเปอร์เซนต์ไทล์ที่ 60 หมายความว่าร้อยละ 60 ของนักศึกษากลุ่มนั้นได้คะแนนวิชาสถิติต่ำกว่า 54

การคำนวณหาคะแนนที่ตำแหน่งคะแนนที่ตำแหน่งเปอร์เซนต์ไทล์ที่กำหนดให้

การดำคำนวณหาคะแนนที่ตำแหน่งเปอร์เซนต์ไทล์ที่กำหนดให้ สามมารถทำได้ 2 วิธี คือ

1.) สำหรับคะแนนที่ไม่ได้จัดหน่วยหมู่ (Ungrouped Data)

2.) สำหรับคะแนนที่จัดหมวดหมู่(Grouped Data)

การคำนวณหาคะคะแนนที่ตำแหน่งเปอร์เซนต์ไทล์ที่กำหมดให้สำหรับข้อมูลที่ไม่ได้จัดหมวดหมู่

ผลการสอบวิชาสถิติของศึกษาชั้นปีที่ 1 จำนวน 20 คน ได้คะแนนดังนี้ต่อไปนี้

67 45 73 78 38 54 61 41 53 36

55 37 74 65 47 34 66 68 77 44

คะแนนเท่าไหร่แสดงว่าศึกษาร้อยละ 75 ของนักศึกษา 20 คนนี้ ได้คะแนนต่ำกว่าคะแนนนั้น

วิธีทำ

1.) เรียงลำดับคะแนนจากน้้อยไปหามาก ดังนี้

34 36 37 38 41 44 45 47 53 54

55 61 65 66 67 68 73 74 77 78

2.) หาตำแหน่งของเปอณเซนต์ไทล์ที่กำนดให้จากตำแหน่งของคะแนนที่เรียงลำดับแล้วให้ข้อ 1.) คะแนนในตำแหน่งเปอร์เซนต์ไทล์ที่ 75 คือ (75 * 20) /100 =15

ดังนั้นจากคะแนนที่เรียงลำดับแล้ว ตำแหน่งที่ 15 คือคะแนน 67

การคำนวณหาคะแนนที่ตำแหน่งเปอร์เซนต์ไทล์ที่กำหมด สามารถทำได้ 3 วิธี คือ

1.) .ใช้สูตร

2.) เทียบบัญญัติไตรยางศ์

3.) ใช้โค้งความถี่สะสม

วิธีการคำนวณคล้สยกับการคำนวณหามัธยฐานต่างกันที่การหาตำแหน่งเปอร์เซ้นต์คะแนนชุดนั้น จะไม่ใช้คะแนนในตำแหน่งกลาง (N/2) เหมือนกับมัธยฐาน ซึ่งสูตรที่ใช้ในการคำนวณตำแหน่งเปอณ์เซ็นต์ไทล์ คือ

Pr = L+I{(F n-F 1)/(F 2-F 1)}

เมื่อ Pr =คะแนนที่ตำแหน่งเปอร์เซนต์ไทล์ที่ต้องกการ

L =ขีดจำกัดล่างชั้นที่มี F n อยู่

I = ความกว้างของอันตราภาคชั้น = ขีดจำกัดบน-ขีดจำกัดล่าง

F n = ความถี่สะสมของตำแหน่งที่ต้องการ = (P*N)/100

F 1 = ความถี่สะสมชั้นที่อยู่ถัดจากชั้น F n ไปทางคะแนนน้อย

F 2 = ความถี่สะสมชั้น F n

คะแนน	ความถี่
10-19	2
20-29	8
30-39	9
40-49	1.4
50-59	8
60-69	6
70-79	3
N = 50

วิธีทำ 1.) ตางรางแจกแจงความถี่สะสมจากคะแนนน้อยไปหาคะแนนมาก

คะแนน	ความถี่	ความถี่สะสม
10-19	2	2
20-29	8	10
30-39	9	19
40-49	1.4	33
50-59	8	41
60-69	6	47
70-79	3	50
N = 50

2.) คำนวณหาความถี่สะสมของตำแหน่งที่ต้องการ(F n) ของคะแนนที่ตำแหน่งเปอร์เซนต์ไทล์ที่กำหมดให้

P 25 ของคะแนนชุดนี้ตรงกับความถี่สะสมของตำแหน่งที่ = (P*N)/100

= (25*50)/100

= 12.5

ดังนั้น F n = 12.5

3.) หาชั้นของคะแนนในตารางความถี่สะสม ที่มีตำแหน่งที่ต้องการ (Fn) อยู่ซึ่งตำแหน่งที่ 12.5 ชั้นที่มีคะแนนระหว่าง 30 – 39 ดังนี้

L = 29.5

I = 19.5-9.5 = 10

F 1= 10

F2=19

4.) คำนวณหาคะแนนในตำแหน่งเปอร์เซนต์ไทล์ที่กำหมด จากสูตร

P = L 1 + I{(F n-F 1) / (F 2-F 1)}

P 25 = 29.5 + 10 {(12.5-10)/(19-10)}

=29.5 + 10 {2.5/9}

=29.5 +2.78

=32.28

การวัดการกระจายของข้อมูล

การวัดการกระจายของข้อมูล
การวัดการกระจายของข้อมูล หมายถึงการคำนวณว่าข้อมูลชุดใดชุดหนึ่งกระจายออกจากกัน หรืออยู่ห่างกันมากน้อยเพียงใด ถ้าคะแนนของข้อมูลในชุดใดอยู่ห่างกันน้อยหรือมีขนาดใกล้เคียงกัน เรียกว่าข้อมูลชุดนั้นมีการกระจายน้อย แต่ถ้าคะแนนของข้อมูลในชุดใดอยู่ห่างกันมาก เรียกว่าข้อมูลชุดนั้นมีการกระจายมาก
การอธิบายลักษณะของข้อมูลโดยวิธีการวัดแนวโน้มเข้าสู่ส่วนกลางเป็นการอธิบาย ลักษณะของข้อมูลเพียงลักษณะเดียว ส่วนลักษณะอื่นๆไม่สามารถแสดงได้ด้วยการวัดแนวโน้มเข้าสู่ส่วนกลาง ตัวอย่าง เช่น
ข้อมูลชุดที่ 1 : 5 11 18 25 41
ข้อมูลชุดที่ 2 : 14 20 21 22 23

มัชฌิมเลขคณิตของข้อมูลชุดที่ 1 = (5 + 11 + 18 + 25 + 41) / 5
= 100 / 5
= 20
มัชฌิมเลขคณิตของข้อมูลชุดที่ 2 = (14 + 20 + 21 + 22 + 23) / 5
= 100 / 5
= 20

จะเห็นว่าค่ามัชฌิมเลขคณิตของข้อมูลทั้งสองชุดมีค่าเท่ากัน โดยที่ลักษณะของข้อมูลทั้งสองชุดต่างกัน ข้อมูลชุดที่ 1 ประกอบด้วยคะแนนที่มีค่าสูงสุดและต่ำสุดแตกต่างกันมาก ส่วนข้อมูลชุดที่ 2 ประกอบด้วยคะแนนที่มีค่าใกล้เคียงกัน ซึ่งการใช้มัชฌิมเลขคณิตเป็นตัวแทนของข้อมูลทั้งสองชุด ทำให้ผู้ที่ไม่ทราบข้อมูลทั้งสองชุดมีความเข้าใจผิดว่าข้อมูลทั้งสองชุดนั้น มีลักษณะเหมือนกัน ดังนั้นจึงจำเป็นต้องมีการวัดการกระจายของข้อมูลด้วย เพื่อทำให้ทราบลักษณะของข้อมูลชัดเจนยิ่งขึ้น
การวัดการกระจายของข้อมูล สามารถทำได้ ดังนี้ คือ

พิสัย (Range)
ส่วนเบี่ยงเบนควอร์ไทล์ (Quartile Deviation)
ส่วนเบี่ยงเบนเฉลี่ย (Mean Deviation or Average Deviation)
ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation)

5.2 พิสัย (Range)
พิสัย หมายถึงความแตกต่างระหว่างคะแนนสูงสุดกับคะแนนต่ำสุดในข้อมูลชุดหนึ่งๆ พิสัยใช้ในการวัดการกระจายของข้อมูลได้ไม่ละเอียดนัก นิยมใช้กรณีเมื่อต้องการความรวดเร็วเท่านั้น ข้อเสียของพิสัยของข้อมูลแต่ละชุด คือมีการใช้เฉพาะคะแนนสูงสุดและคะแนนต่ำสุดเท่านั้น บางครั้งทำให้เกิดการเข้าใจถึงลักษณะของข้อมูลผิดไปได้ ตัวอย่าง เช่น

ข้อมูลชุดที่ 1 : 5 30 32 39 42 50
ข้อมูลชุดที่ 2 : 42 44 46 48 49 51

พิสัยของข้อมูลชุดที่ 1 = 50 – 5 = 45
พิสัยของข้อมูลชุดที่ 2 = 51 – 42 = 9

จะเห็นว่าพิสัยของข้อมูลทั้งสองชุดต่างกันมาก ทั้งๆที่ข้อมูลทั้งสองชุดนั้นมีลักษณะคล้ายคลึงกันมาก

7.ค่ามาตรฐาน พื้นที่ใต้เส้นโค้งปกติ

ค่ามาตรฐาน หรือ คะแนนมาตรฐาน เป็นค่าที่เราสามารถเอาไว้เปรียบเทียบข้อมูลระหว่างชุดได้ เพราะถ้าเรานำข้อมูลสองชุดมาเปรียบเทียบกัน

เส้นโค้งปกติมาตรฐาน

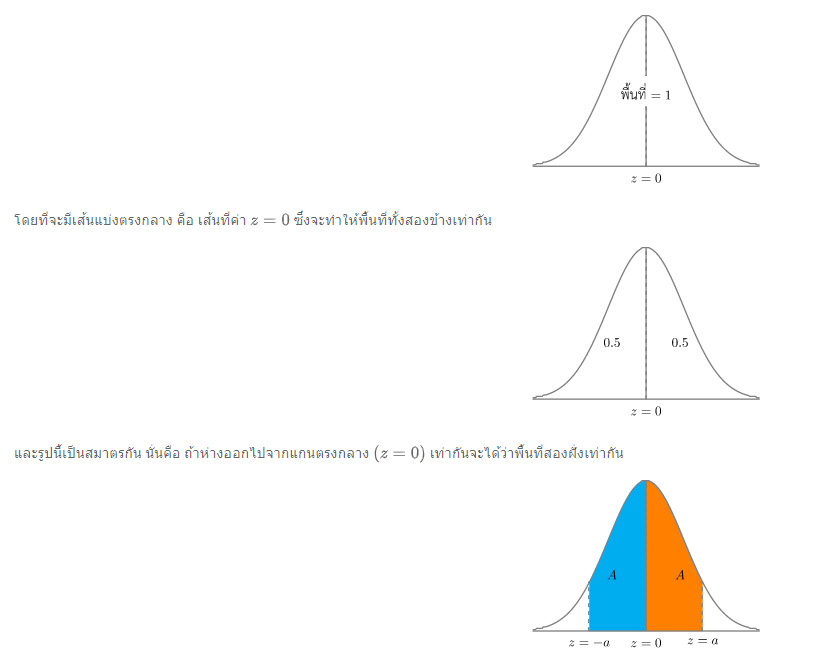
เส้นโค้งปกติมาตรฐาน คือ เส้นโค้งที่มีรูปร่างเป็นรูประฆังคว่ำและพื้นที่ใต้กราฟทั้งหมดเท่ากับ $1$ โดยค่ามาตรฐาน $(z)$ จะเป็นค่าที่แสดงในแนวแกน $x$
โดยที่จะมีเส้นแบ่งตรงกลาง คือ เส้นที่ค่า $z = 0$ ซึ่งจะทำให้พื้นที่ทั้งสองข้างเท่ากัน
และรูปนี้เป็นสมาตรกัน นั่นคือ ถ้าห่างออกไปจากแกนตรงกลาง $(z = 0)$ เท่ากันจะได้ว่าพื้นที่สองฝั่งเท่ากัน