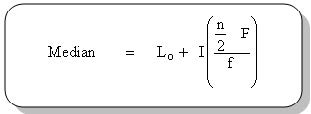สรุปเนื้อหา สถิติ ม.6
สรุปสูตร สถิติ ทั้งหมด
1) ค่าเฉลี่ยเลขคณิต
2) มัธยฐาน
3) ฐานนิยม
4) ควอไทล์ เดไซล์ เปอร์เซนไทล์
5) การวัดการกระจาย
6) ความแปรปรวน และความแปรปรวนรวม
7) ค่ามาตรฐาน พื้นที่ใต้เส้นโค้งปกติ
9) ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล
แผนภาพกล่อง เป็นการนำเสนอข้อมลู โดยนำค่าต่ำสุด ค่าสูงสุด ควอร์ไทล์ที่หนึ่ง ควอร์ไทล์ที่สอง และ ควอร์ไทล์ที่สาม มาสร้างเป็นรูปส่ีเหล่ียมผืนผ้า 2 รูปติดกัน จากการแบ่งข้อมูลทีมีการจัดเรียงลำดับค่าจากน้อยไปมาก แล้วแบ่งข้อมลู ออกเป็น 4 ส่วนเท่า ๆ กัน ซึ่ง แต่ละส่วนคิดเป็น ร้อยละ 25 ของจำนวนข้อมูลทั้งหมด
การอ่านและการแปลความแผนภาพกล่อง เป็น ดังนี้
1. การกระจายแบบเบ้ขวา คือ ข้อมูล ท่ีอยู่ระหว่าง Q1 กับ Q2 มีการกระจายน้อยกว่า
ข้อมูลที่อยู่ระหว่าาง Q2 กับ Q3 (พ้ืนทีของรูปสี่เหลี่ยมผืนผ้าทางด้านซ้าย น้อยกว่าด้านขวา)
2. การกระจายแบบเบซ้ ย คือ ข้อมูล ที่อยู่ระหว่าง Q1 กับ Q2 มีการกระจายมากกว่าข้อมูลทที่อยู่ระหว่าง Q2 กับ Q3 (พื้นที่ของรูปสี่เหลี่ยมผืนผ้าทางด้านซ้ายมากกว่าด้านขวา)
3. การกระจายแบบปกติ คือ ข้อมูลที่อยู่ระหว่าง Q1 กับ Q2 มีการกระจายเท่ากับข้อมูลที่อยู่ระหว่าง Q2 กับ Q3 (พื้นท่ีของรูปสี่เหลียมผืนผ้าทางด้านซ้ายเท่ากับ ด้านขวา)
ค่าเฉลี่ยเลขคณิต (Arithmetic Mean , Average , )
)
ค่าเฉลี่ยเลขคณิต( ) จัดว่าเป็นค่าที่มีความสำคัญมากในวิชาสถิติ เพราะค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทนของข้อมูลที่ดีที่สุด เพราะ 1)เป็นค่าที่ไม่เอนเอียง 2)เป็นค่าที่มีความคงเส้นคงวา 3)เป็นค่าที่มีความแปรปรวนต่ำที่สุด และ 4)เป็นค่าที่มีประสิทธิภาพสูงสุด แต่ค่าเฉลี่ยเลขคณิตก็มีข้อจำกัดในการใช้ เช่น ถ้าข้อมูลมีการกระจายมาก หรือข้อมูลบางตัวมีค่ามากหรือน้อยจนผิดปกติ หรือข้อมูลมีการเพิ่มขึ้นเป็นเท่าตัว ค่าเฉลี่ยเลขคณิตจะไม่สามารถเป็นค่ากลางหรือเป็นตัวแทนที่ดีของข้อมูลได้
) จัดว่าเป็นค่าที่มีความสำคัญมากในวิชาสถิติ เพราะค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทนของข้อมูลที่ดีที่สุด เพราะ 1)เป็นค่าที่ไม่เอนเอียง 2)เป็นค่าที่มีความคงเส้นคงวา 3)เป็นค่าที่มีความแปรปรวนต่ำที่สุด และ 4)เป็นค่าที่มีประสิทธิภาพสูงสุด แต่ค่าเฉลี่ยเลขคณิตก็มีข้อจำกัดในการใช้ เช่น ถ้าข้อมูลมีการกระจายมาก หรือข้อมูลบางตัวมีค่ามากหรือน้อยจนผิดปกติ หรือข้อมูลมีการเพิ่มขึ้นเป็นเท่าตัว ค่าเฉลี่ยเลขคณิตจะไม่สามารถเป็นค่ากลางหรือเป็นตัวแทนที่ดีของข้อมูลได้
การหาค่าเฉลี่ยเลขคณิตเมื่อข้อมูลไม่ได้มีการแจกแจงความถี่ ( )
)
ในกรณีที่ข้อมูลไม่ได้มีการแจกแจงความถี่ ค่าเฉลี่ยเลขคณิตสามารถหาได้โดย
สูตร

1) ฐานนิยม (Mode)
ฐานนิยม (Mode : Mo) หมายถึง ค่าของข้อมูลในชุดใดชุดหนึ่ง ซึ่งมีความถี่สูงที่สุดหรือซ้ำกันมากที่สุด การหาฐานนิยมแบ่งเป็น 2 กรณี
1.1) กรณีที่ข้อมูลไม่จัดเป็นกลุ่ม
Ex.
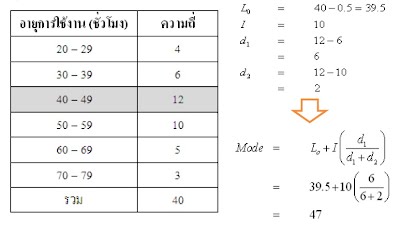
1.2) กรณีที่ข้อมูลจัดเป็นกลุ่ม
หาได้จากสูตร
Ex. จงหาฐานนิยมของข้อมูลต่อไปนี้
มัธยฐาน (Median)
มัธยฐาน (Median : Md) คือ ค่าที่อยู่ตรงกลางของชุดข้อมูลหลังจากทำการเรียงลำดับแล้ว มัธยฐานเป็นค่าที่แบ่งข้อมูลออกเป็นสองส่วน ส่วนหนึ่งมีค่าน้อยกว่าค่ามัธยฐาน อีกส่วนหนึ่งมีค่ามากกว่ามัธยฐาน การหามัธยฐานแบ่งเป็น 2 กรณี
2.1) กรณีที่ข้อมูลไม่แจกแจงความถี่
Ex. จงหามัธยฐานของข้อมูลต่อไปนี้
1) 45 20 30 55 40 50 60
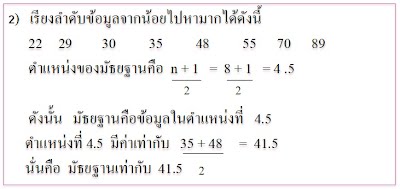
2) 48 22 30 55 70 89 29 35
2.2) กรณีที่ข้อมูลแจกแจงความถี่
2.2.1) เรียงลำดับข้อมูลจากน้อยไปหามากโดยการหาความถี่สะสมจากน้อยไปมาก
2.2.2) หาตำแหน่งของมัธยฐานจาก n/2 เมื่อ n แทนจำนวนข้อมูลทั้งหมด
2.2.3) หาค่าของตำแหน่งที่คำนวณได้จากข้อ 2 โดยสูตร
L0 แทน ขอบเขตล่างของชั้นมัธยฐาน
I แทน ความกว้างของชั้นมัธยฐาน n แทน จำนวนข้อมูลทั้งหมด
F แทน ความถี่สะสมแบบน้อยกว่าจนถึงชั้นก่อนมัธยฐาน
f แทน ความถี่ของชั้นมัธยฐาน
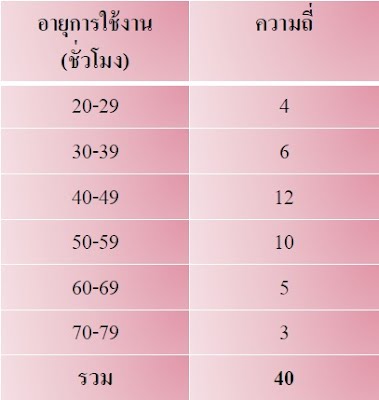
หาความถี่สะสมแบบน้อยกว่าของข้อมูล
ตำแหน่งมัธยฐาน = n/2 = 40/2 = 20
ตำแหน่งที่ 20 มีคะแนนอยู่ในช่วง 40 – 49 ดังนั้นชั้น 40 – 49 เป็นชั้นมัธยฐาน
Ex. จงหามัธยฐานของข้อมูลต่อไปนี้
หาความถี่สะสมแบบน้อยกว่าของข้อมูล
ตำแหน่งมัธยฐาน = n/2 = 40/2 = 20
ตำแหน่งที่ 20 มีคะแนนอยู่ในช่วง 40 – 49 ดังนั้น ชั้น 40 – 49 เป็นชั้นมัธยฐาน
ความแปรปรวน และความแปรปรวนรวม
![]() )
)![]() ) จัดว่าเป็นค่าที่มีความสำคัญมากในวิชาสถิติ เพราะค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทนของข้อมูลที่ดีที่สุด เพราะ 1)เป็นค่าที่ไม่เอนเอียง 2)เป็นค่าที่มีความคงเส้นคงวา 3)เป็นค่าที่มีความแปรปรวนต่ำที่สุด และ 4)เป็นค่าที่มีประสิทธิภาพสูงสุด แต่ค่าเฉลี่ยเลขคณิตก็มีข้อจำกัดในการใช้ เช่น ถ้าข้อมูลมีการกระจายมาก หรือข้อมูลบางตัวมีค่ามากหรือน้อยจนผิดปกติ หรือข้อมูลมีการเพิ่มขึ้นเป็นเท่าตัว ค่าเฉลี่ยเลขคณิตจะไม่สามารถเป็นค่ากลางหรือเป็นตัวแทนที่ดีของข้อมูลได้
) จัดว่าเป็นค่าที่มีความสำคัญมากในวิชาสถิติ เพราะค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทนของข้อมูลที่ดีที่สุด เพราะ 1)เป็นค่าที่ไม่เอนเอียง 2)เป็นค่าที่มีความคงเส้นคงวา 3)เป็นค่าที่มีความแปรปรวนต่ำที่สุด และ 4)เป็นค่าที่มีประสิทธิภาพสูงสุด แต่ค่าเฉลี่ยเลขคณิตก็มีข้อจำกัดในการใช้ เช่น ถ้าข้อมูลมีการกระจายมาก หรือข้อมูลบางตัวมีค่ามากหรือน้อยจนผิดปกติ หรือข้อมูลมีการเพิ่มขึ้นเป็นเท่าตัว ค่าเฉลี่ยเลขคณิตจะไม่สามารถเป็นค่ากลางหรือเป็นตัวแทนที่ดีของข้อมูลได้![]() )
)