George Cantor นักคณิตศาสตร์ผู้ให้กำเนิดทฤษฎีเซ็ตที่มีอิทธิพลต่อคณิตศาสตร์ในคริสต์ศตวรรษที่ 20 มาก
วงการคณิตศาสตร์เมื่อ 150 ปีก่อน มีอัจฉริยะที่เด่นสุดยอดท่านหนึ่ง ชื่อ George Cantor ผู้ให้กำเนิดทฤษฎีเซ็ตที่มีอิทธิพลต่อคณิตศาสตร์ในคริสต์ศตวรรษที่ 20 มาก ผลงานนี้ทำให้ David Hilbert กล่าวสรรเสริญ Cantor ว่า เขาคือผู้สร้างสวนสวรรค์ Eden ให้นักคณิตศาสตร์รุ่นหลังได้อยู่ทำงานในสวนอย่างมีความสุข จนแม้แต่พระเจ้าก็ไม่ทรงสามารถอัปเปหิใครออกจากสวนได้ แต่ทว่าในช่วงที่มีชีวิตอยู่ Cantor ถูกนักคณิตศาสตร์อาวุโสหลายคนต่อต้าน และโจมตีเพราะคิดว่า Cantor ชอบเสนอแนวคิดเกี่ยวกับทฤษฎีเซ็ตและเรื่องอนันต์ (infinity) ที่ผิด แม้ชีวิตของ Cantor ต้องลำบากเพราะประสบอุปสรรคมากมาย แต่โลกทุกวันนี้ก็ยังระลึกถึง เขาผู้ให้กำเนิดวิชาคณิตศาสตร์แขนงใหม่ คือ ทฤษฎีเซ็ต
บิดาของ คันทอร์ มีชื่อว่า จอร์จ วอลด์มาร์ คันทอร์ (George Waldemar Cantor) เป็นพ่อค้าชาวเดนมาร์ก ที่ประสบความสำเร็จทางการค้าในเซนต์ปีเตอร์สเบิร์ก มารดาเป็นชาวรัสเซีย มีชื่อว่า Maria Anna Bohm เมื่อ คันทอร์มีอายุได้ 11 ปี ครอบครัวของเขาจึ่งย้ายไปเยอรมนี ในวัยเรียน คันทอร์เป็นเด็กที่มีผลการเรียนในระดับดีเยี่ยม โดยเฉพาะอย่างยิ่งในวิชาตรีโกณมิติ ต่อมาได้เข้าศึกษาต่อใน Höherem Gewerbeschule แห่งเมื่องดามชตัดท์ และ ในปี ค.ศ. 1862 ย้ายไป สถาบันเทคโนโลยีสวิส ซูริค (Polytechnic of Zurich) ที่ซึ่งเขาเลือกเรียนทางด้านวิศวกรรมศาสตร์ตามความต้องการของบิดา และภายหลังจึงย้ายมาเรียนคณิตศาสตร์ตามความชอบของตนแทน ต่อมาเมือบิดาเสียชีวิตลง คันทอร์ จึงย้ายมาเรียนที่ มหาวิทยาลัยฮุมโบลด์ทแห่งเบอร์ลิน (University of Berlin) จนสำเร็จการศึกษาในปี ค.ศ. 1867 โดยมีหัวข้อวิทยานิพนธ์ทางด้านทฤษฎีจำนวน หลังจากสำเร็จการศึกษาแล้ว จึงเป็นครูสอนคณิตศาสตร์ในโรงเรียนและย้ายมาเป็นอาจารย์ประจำที่ Halle university ในปี ค.ศ. 1869
ตอนเริ่มแรกของ Beitrge zur Begrndung der transfiniten Mengenlehre โดย เกออร์ก คันทอร์ (Georg Cantor) ผู้สร้าง
ทฤษฎีเซตคนสำคัญ ให้นิยามของเซตเซตหนึ่งดังต่อไปนี้
โดย “เซต” เซตหนึ่ง เราหมายถึงการสะสมรวบรวมใดๆ ที่ให้ชื่อว่า M เข้าเป็นหน่วยเดียวกันทั้งหมด ของวัตถุที่ให้ชื่อว่า m ที่แตกต่างกัน (ซึ่งเรียกว่า “สมาชิก” ของ M) ตามความเข้าใจของเรา หรือตามความคิดของเรา
ดังนั้นสมาชิกของเซตเซตหนึ่งจึงสามารถเป็นอะไรก็ได้ เช่น ตัวเลข ผู้คน ตัวอักษร หรือเป็นเซตของเซตอื่น เป็นต้น เซตนิยมเขียนแทนด้วยอักษรตัวใหญ่ เช่น A, B, C ฯลฯ ตามธรรมเนียมปฏิบัติ ในประโยคที่ว่า เซต A และ B เท่ากัน หมายความว่า ทั้งเซต A และเซต B มีสมาชิกทั้งหมดเหมือนกัน (ตัวอย่างเช่น สมาชิกทุกตัวที่อยู่ในเซต A ก็ต้องเป็นสมาชิกของเซต B ด้วย เขียนแทนด้วย A = B และในทางกลับกันก็เป็นเช่นเดียวกัน เขียนแทนด้วย B = A)
สมาชิกทุกตัวของเซตเซตหนึ่งต้องไม่ซ้ำกัน และจะไม่มีสมาชิกสองตัวใดในเซตเดียวกันที่เหมือนกันทุกประการ ซึ่งไม่เหมือนกับมัลทิเซต (multiset) ที่อาจมีสมาชิกซ้ำกันก็ได้ การดำเนินการของเซตทั้งหมดยังรักษาคุณสมบัติที่ว่าสมาชิกแต่ละตัวของเซตต้องไม่ซ้ำกัน ส่วนการเรียงลำดับของสมาชิกของเซตนั้นไม่มีความสำคัญ ซึ่งต่างจากลำดับอนุกรมหรือคู่อันดับ
ถึงอย่างไรก็ตามเซตถือว่าเป็น อนิยาม ไม่มีนิยามที่ชัดเจนและครอบคลุม

ความเข้าใจเบื้องต้นของเซต เซต คือกลุ่มของสมาชิก
เซต = { สมาชิก } การเขียนเซต สามารถเขียนได้ 2 แบบ
1. การเขียนแบบแจกแจงสมาชิก เช่น เซตของจำนวนนับที่น้อยกว่า 6 เขียนแทนด้วย {1,2,3,4,5}
2. การเขียนแบบบอกเงื่อนไข เช่น {x| x เป็นเดือนแรกและเดือนสุดท้ายของปี } = {เดือนมกราคม,เดือนธันวาคม}
ในการเขียนเซตโดยที่ทั่วไปจะแทนเซตด้วยอักษรภาษาอังกฤษตัวพิมพ์ใหญ่ เช่น A,B,C และใช้สัญลักษณ์“ € ” แทนคำว่าเป็นสมาชิกหรืออยู่ในเซต
เช่น A = {1,2,3,4} จะได้ว่า 1 € A และจะใช้ n แทนจำนวนสมาชิกที่อยู่ในเซตนั้นๆ เช่น A = {1,2,3,4} n(A) = 4
เซต แบ่งออกได้เป็น 2 อย่าง คือ 1. เซตจำกัด คือ เซตที่สามารถนับจำนวนสมาชิกได้ทั้งหมดและมีจำนวนที่แน่นอน เช่น A = {1,2,3,4}
2. เซตอนันต์ คือ เซตที่ไม่สามารถบอกจำนวนสมาชิกได้เพราะสมาชิกมีจำนวนมาก เช่น A = {1,2,3,4,…}

การกระทำระหว่างเซต
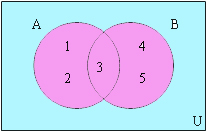
ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B ตัวอย่างเช่น A ={1,2,3} B= {3,4,5}   ∴ A ∪ B = {1,2,3,4,5}
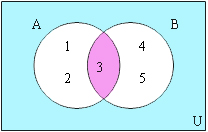
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B ตัวอย่างเช่นA ={1,2,3}B = {3,4,5}∴ A ∩ B = {3}
คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’ตัวอย่างเช่น U = {1,2,3,4,5} A ={1,2,3} ∴ A’ = {4,5}
สับเซต (Subset) ใช้สัญลักษณ์ ⊂ หมายถึง เป็นสับเซต ⊄ หมายถึง ไม่เป็นสับเซต A ⊂ B ก็ต่อเมื่อ สมาชิกทุกตัวในเซต A เป็นสมาชิกทุกตัวในเซต B เช่น A= {1,2,3} B= {1,2,3,4,5} A ⊂ B เพราะ สมาชิกทุกตัวในเซต A เป็นสมาชิกที่อยู่ในเซต B
C= {1,2} D= {3,4,5} A⊄B เพราะ ไม่มีสมาชิกในเซตC เป็นสมาชิกในเซต D

การเขียนเซต

การเขียนเซตอาจเขียนได้ 2  แบบ

1 การเขียนซตแบบแจกแจงสมาชิก  เขียนสมาชิกทุกตัวลงในเครื่องหมายวงเล็บปีก กา { }  และใช้เครื่องหมายจุลภาค ( , ) คั่นระหว่างสมาชิกแต่ละตัว  เช่น

  เซตของจำนวนนับที่น้อยกว่า  7  เขียนแทนด้วย  {1,2,3,4,5,6,}

เซตของพยัญชนะไทย  5  ตัวแรก  เขียนแทนด้วย  { ก,ข,ฃ,ค,ฅ }

2.เขียนแบบบอกเงื่อนไข  ใช้ตัวแปรเขียนแทนสมาชิกของเซต  แล้วบรรยายสมบัติของสมาชิกที่อยู่รูปของตัวแปร  เช่น

{x| x เป็นสระในภาษาอังกฤษ } อ่านว่า เซตของ x โดยที่ x เป็นสระในภาษาอังกฤษ

{x| x  เป็นเดือนแรกและเดือนสุดท้ายของปี } อ่านว่า เซตของ xโดยที่ x เป็นเดือนแรกและเดือนสุดท้ายของปี  เครื่องหมาย “ | ”  แทนคำว่า  โดยที่

ในการเขียนเซตแบบแจกแจงสมาชิกนั้นจะใช้จุด ( … )  เพื่อแสดงว่ามีสมาชิกอื่นๆ ซึ่งเป็นที่เข้าใจกันทั่วไปว่ามีอะไรบ้างที่อยู่ในเซต  เช่น

{ 1,2,3,…,10 }  สัญลักษณ์ … แสดงว่ามี 4,5,6,7,8 และ9 เป็นสมาชิกของเซต

{ วันจันทร์, อังคาร, พุธ,…, อาทิตย์ } สัญลักษณ์ … แสดงว่ามีวันพฤหัสบดี  วันศุกร์  และวันเสาร์  เป็นสมาชิกของเซต

 สัญลักษณ์แทนเซต 

ในการเขียนเซตโดยที่ทั่วไปจะแทนเซตด้วยอักษรภาษาอังกฤษตัวพิมพ์ใหญ่  เช่น A,B,C และแทนสมาชิกของเซตด้วยตัวพิมพ์เล็ก เช่น a,b,c เช่น

A = {1,4,9,16,25,36}  หมายถึง A เป็นเซตของกำลังสองของจำนวนนับหกจำนวนแรก }

สมาชิกของเซต

จะใช้สัญลักษณ์ “  € ”  แทนคำว่าเป็นสมาชิกหรืออยู่ใน  เช่น

A = {1,2,3,4}

จะได้ว่า  1   เป็นสมาชิกของ  A หรืออยู่ใน A เขียนแทนด้วย  1  €A

3   เป็นสมาชิกของ  A  หรืออยู่ใน A เขียนแทนด้วย  3€ A

คำว่า “ม่เป็นสมาชิก” หรือ “ไม่อยู่ใน”  เขียนด้วยสํญลักษณ์  “ € ”  เช่น

5  ไม่เป็นสมาชิกของ A หรือไม่อยู่ใน A เขียนแทน 5€A

7 ไม่เป็นสมชิกชอง A หรือไม่อยู่ใน A เขียนแทนด้วย  7€A

สำหรับเซต A ซึ่งมีสมาชิก 4 ตัว เราจะใช้ n(A) เพื่อบอกจำนวนสมาชิกของเซต A นั่นคือ n(A) = 4

ตัอย่างที่ 1   จงเขียนเซตต่อไปนี้แบบแจกแจงสมาชิก

1.เซตของจังหวัดในประเทศไทยที่ลงท้ายด้วยบุรี

2.ซตของจำนวนเมลบ

3.เซตของพยัญชนะในภาษาไทย

วิธีทำ           1.ให้  A เป็นเซตของจังหวัดในประเทศไทยที่ลงท้ายด้วยบุรี

A = {  สุพรรณบุรี, ปราจีนบุรี, สิงห์บุรี,…, ลพบุรี }

2. ให้ B เป็นเซตของจำนวนต็มลบ

B = {-1,-2,-3,…}

3. ให้C เป็นเซตของพยัญชนะในภาษาไทย

C = {ก,ข,ค,…,ฮ}

1. เซตจำกัด (Finite Set)

2. เซตอนันต์ (Infinite Set)

เซตว่าง (Empty Set)

เอกภพสัมพัทธ์ (Relative Universe)

ยูเนียน (Union)

อินเตอร์เซกชัน (Intersection)

คอมพลีเมนต์ (Complements)

ที่มาของเนื้อหา

http://www.manager.co.th/science/เซต