กราฟเส้นตรง

กราฟเส้นตรง

1. สมการของกราฟเส้นตรงที่ขนานกับแกน x
กำหนดให้ L เป็นเส้นตรงที่ขนานกับแกน x ดังนั้น เส้นตรง L ย่อมตั้งฉากกับแกน y และกำหนดให้เส้นตรง L ตัดแกน y ที่จุด (0, b)
ถ้า b > 0 เส้นตรง L จะอยู่เหนือแกน x และห่างจากแกน x เป็นระยะ |b| หน่วย
ถ้า b = 0 เส้นตรง L จะทับแกน x
ถ้า b < 0 เส้นตรง L จะอยู่ใต้แกน x และห่างจากแกน x เป็นระยะ |b| หน่วย

ตัวอย่างเช่น
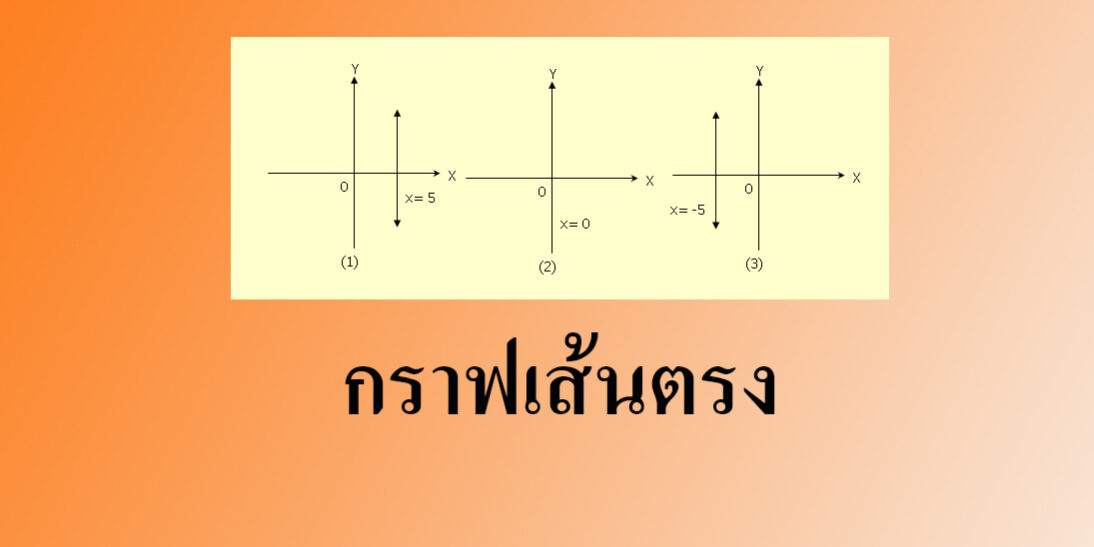
(1) เส้นตรงที่ขนานกับแกน x และอยู่เหนือแกน x เป็นระยะ 5 หน่วย มีสมการเป็น y = 5
(2) เส้นตรงที่ขนานกับแกน x และทับแกน x มีสมการเป็น y = 0
(3) เส้นตรงที่ขนานกับแกน x และอยู่ใต้แกน x เป็นระยะ 5 หน่วย มีสมการเป็น y = -5

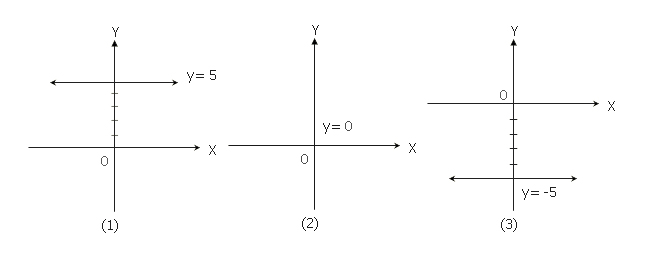
 2. สมการของกราฟเส้นตรงที่ขนานกับแกน y
กำหนดให้ L เป็นเส้นตรงที่ขนานกับแกน y ดังนั้น เส้นตรง L ย่อมตั้งฉากกับแกน x และกำหนดให้เส้นตรง Lตัดกับแกน x ที่จุด (a, 0)
ถ้า a > 0 เส้นตรง L จะอยู่ทางขวาของแกน y และห่างจากแกน y เป็นระยะ |a| หน่วย
ถ้า a = 0 เส้นตรง L จะทับแกน y
ถ้า a < 0 เส้นตรง L จะอยู่ทางซ้ายของแกน y และห่างจากแกน y เป็นระยะ |a| หน่วย

 ตัวอย่างเช่น
(1) เส้นตรงที่ขนานกับแกน y และอยู่ทางขวาของแกน y เป็นระยะ 5 หน่วย มีสมการเป็น x = 5
(2) เส้นตรงที่ขนานกับแกน y และทับแกน y มีสมการเป็น x = 0
(3) เส้นตรงที่ขนานกับแกน y และอยู่ทางซ้ายของแกน y เป็นระยะ 5 หน่วย มีสมการเป็น x = -5

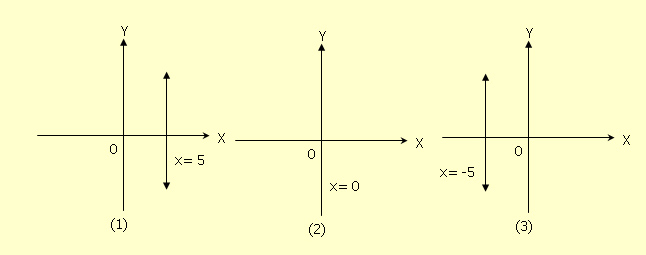
 3. สมการของกราฟเส้นตรงที่ไม่ขนานกับแกน x และไม่ขนานกับแกน y
กำหนดให้ L เป็นเส้นตรงที่ไม่ขนานกับแกน x และไม่ขนานกับแกน y มีความชัน = m และผ่านจุด (x1, y1)

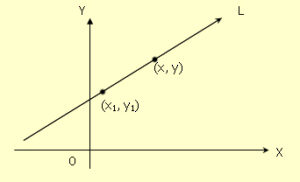
จากรูปให้ (x, y) เป็นจุดใดๆบนเส้นตรง L
∴ ความชันของเส้นตรง L ที่ลากผ่านจุด (x1, y1) และ (x, y) เท่ากับ  (y – y1)  / (x – x 1)

∴     (y – y1)  / (x – x 1) = m
(y – y1) = m(x – x 1)

ตัวอย่างเช่น
(1) สมการของกราฟเส้นตรงที่มีความชันเท่ากับ และผ่านจุด (1, 2) คือ   y – 2 = (x-1)   หรือ 2x – 3y +4 = 0