โดเมนและเรนจ์ ( Domain and Range )
“เรนจ์” ของความสัมพันธ์ 𝑟 แทนด้วยสัญลกษณ R𝑟 หมายถึง เซตกลุ่มตัวหลัง
“เฉพาะตัวที่ถูกโยง”เช่น ถาย้อนกลับไปดูความสัมพันธ์ 𝑟แอบชอบ กับ 𝑟ชกโดน ในหัวข้อก่อนหน้า จะได้โดเมน และ เรนจ์ ดังนี้

D𝑟 = { สมชาย , สมหวัง , สมบัติ }
R𝑟 = { สมหญิง , สมศีร }
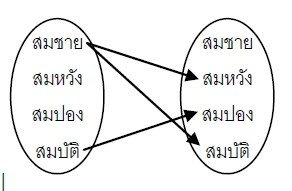
D𝑟 = { สมชาย , สมบัติ }R𝑟 = { สมหวัง , สมปอง , สมบัติ }
ตัวอย่างคู่อันดับ ที่อยู่ใน 𝑟 เช่น (0, 0) , (2,4) , (√3, 2√3) , ( 32 , 3) ,
(− 72 , −7)
จะเห็นว่า 𝑥 กับ 𝑦 เป็นอะไรก็ได้ เราหาคู่ให้ทุกตัว ได้เสมอ
ดังนั้น D𝑟 = R และ R𝑟 = R
ตัวอย่าง กำหนดให้ 𝑟 = { (𝑥, 𝑦) ∈ R 𝑥 R | 𝑦 = 𝑥2} จงหา D𝑟 และ R𝑟
วิธีทำ ตัวอย่างคู่อันดับที่อยู่ใน 𝑟 เช่น (1, 1) , (−3, 9) , (√2, 2) , (−√3, 3)
ดังนั้น D𝑟 = R และ R𝑟 = R+∪ {0}
ถ้าจะหาเรนจ์ ต้องจัดรูปสมการ แยก 𝑥 ทิ้งไปอีกฝั่ง
สมการส่วนใหญที่โจทย์ให้ จะมี 𝑦 แยกทิ้งไปอีกฝั่งอยู่แล้ว ถ้าจะหาโดเมนก็ไม่ต้องจัดรูป
จะเป็นรูปที่หาโดเมนได้เลยแต่ถ้าจะหาเรนจ์ เรามักต้องออกแรงแยก 𝑥 ทิ้งไปอีกฝั่ง
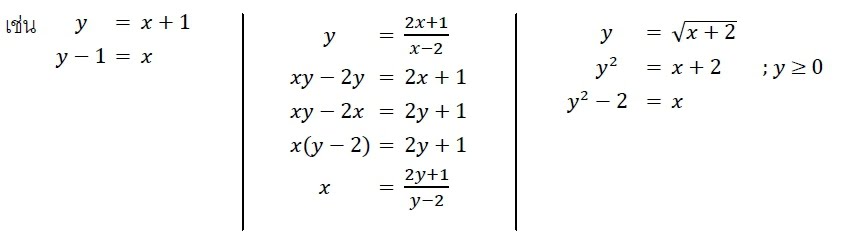
ยกกำลังสองทั้งสองข้าง หรือ ถอดรูททั้งสองข้าง เช่น

ขั้นที่ 2: หาว่า 𝑥 กับ 𝑦 เป็นอะไรได้บ้าง → ส่วน หรือ ตัวหาร ห้ามเป็นศูนย์
→ ข้างใน √ ห้ามติดลบ
𝑥 ≠ 3 → D𝑟 = R − {3}
𝑥 = √𝑦 + 2 → 𝑦 + 2 ≥ 0 → R𝑟 = [−2, ∞)
𝑦 ≥ −2
𝑥 = 3𝑦 → 𝑦 + 2 > 0
√𝑦+2 𝑦 > −2 → R𝑟 = (−2, ∞)
R+∪ {0} → จำนวนจริงบวกทุกตัว รวม 0 ด้วย
[2, 5] → ทุกจำนวน ตังแต่ 2 ถึง 5 (รวม 2 กับ 5 ด้วย) [2, 5) → ทุกจำนวน ตังแต่ 2 ถึง 5 (รวม 2 แต่ไม่รวม 5)
(2, 5] → ทุกจำนวน ตงแต่ 2 ถึง 5 (ไม่รวม 2 แต่รวม 5)
(2, 5) → ทุกจำนวน ระหว่าง 2 กับ 5 (ไม่รวม 2 ไม่รวม 5)
(−∞, 1] → ทุกจำนวน ที่ ≤ 1 [1, ∞) → ทุกจำนวน ที่ ≥ 1
(−∞, 1) → ทุกจำนวน ที่ < 1 (1, ∞) → ทุกจำนวน ที่ >1
(−∞, 2) ∪ [5, ∞) → ทุกจำนวน ที่ < 2 หรือ ≥ 5
ตัวอย่าง จงหาโดเมน และ เรนจ์ ของความสัมพันธ์ 𝑦 = 𝑥2− 6𝑥 + 5
วิธทำ สมการที่โจทย์ให้ อยู่ในรูปที่หาโดเมนได้เลย
จะเห็นว่าข้อนี้ 𝑥 ไม่เป็นตัวหาร และ ไม่อยู่ใน √ ดังนั้น 𝑥 เป็นได้ทุกอย่าง จะได้ D𝑟 = R
ถัดมา หาเรนจ์ ต้องจัดรูป แยก 𝑥 ทิ้งไปอีกฝั่ง
ข้อนี้ จัดรูปยากหน่อย เพราะมีทั้ง 𝑥 กำลังสอง และ 𝑥 กำลังหนึ่ง
เราต้องใช้กำลังสองสมบรูณ์ มารวบ 𝑥2กับ 4𝑥 เข้าด้วยกัน ให้เหลือ 𝑥 เดียวก่อน ดังนี้
น2 +- 2นล + ล2 = (น +- ล)2 𝑦 = 𝑥2− 6𝑥 + 5
𝑦 = 𝑥2− 2(𝑥)(3) + 32− 32+ 5
𝑦 = (𝑥 − 3)2− 4
จากนั้น จึงจัดรูป แยก 𝑥 ทิ้งไปอีกฝั่ง ดังนี้ 𝑦 + 4 = (𝑥 − 3)2 +-√𝑦 + 4 = 𝑥 − 3
+-√𝑦 + 4 + 3 = 𝑥
เนื่องจากใน √ ห้ามตัดลบ ดังนั้น 𝑦 + 4 ≥ 0
𝑦 ≥ −4 จะได้ R𝑟 = [−4, ∞)






