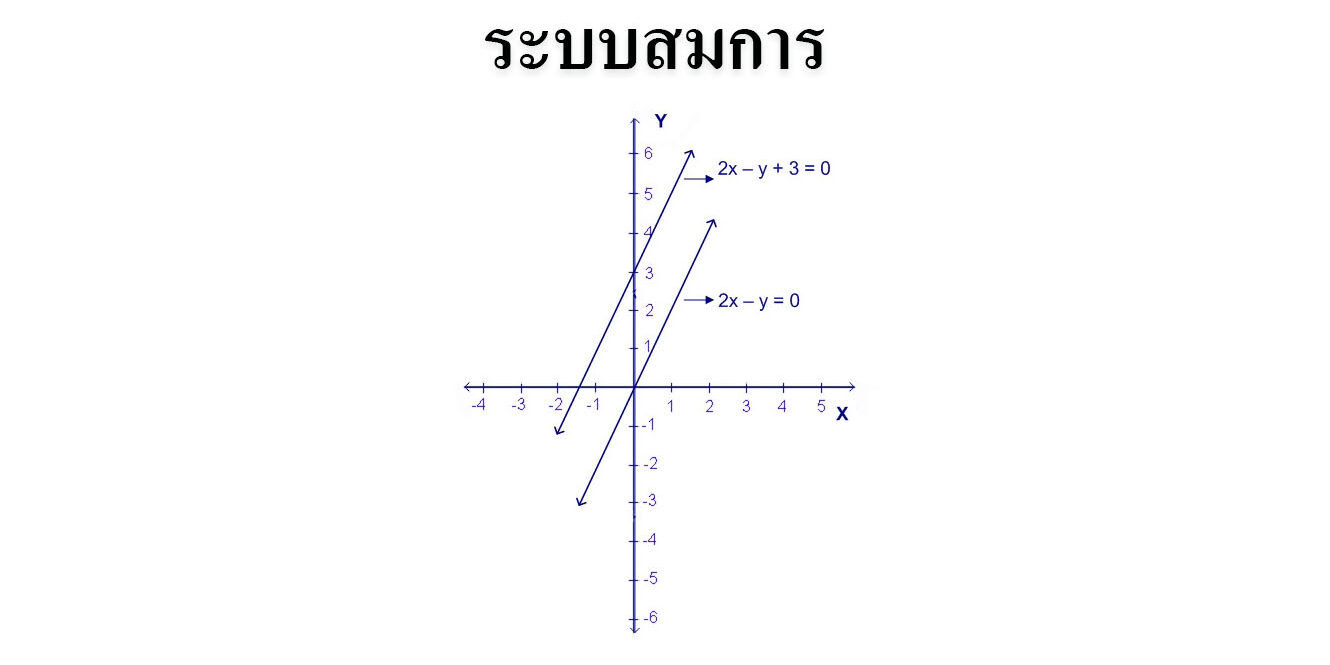
ระบบสมการ

ระบบสมการเชิงเส้นสองตัวแปร

ข้อสังเกตของสมการเชิงเส้นสองตัวแปร Ax + By + C  =  0

1) มีตัวแปรสองตัว คือ x และ y

2) ไม่มีการคูณกันของตัวแปร (ไม่มี xy)

3) เลขชี้กำลังของตัวแปรแต่ละตัวเป็นหนึ่ง

4) สัมประสิทธิ์ของตัวแปรใดตัวแปรหนึ่งเป็นศูนย์ได้ แต่ไม่เป็นศูนย์พร้อมกันเช่น เมื่อ A  =  0

สมการอยู่ในรูป By + C  =  0

เมื่อ B  =  0  สมการอยู่ในรูป Ax + C  =  0

5) ถ้าไม่ระบุเงื่อนไขของ x และ y ให้ถือว่า x และ y เป็นจำนวนจริงใดๆ

6) กราฟของสมการเชิงเส้นสองตัวแปรเป็นเส้นตรง เรียกว่า กราฟเส้นตรง

ระบบสมการเชิงเส้นสองตัวแปร หมายถึง สมการเชิงเส้นที่มีตัวแปรสองตัวและมีจำนวนสมการจำกัดมากกว่าหรือเท่ากับ 1 สมการ
ถ้า a, b, c, d, e และ f เป็นจำนวนจริงใด ๆ ที่ a และ b ไม่เป็นศูนย์พร้อมกันและ c, d ไม่เป็นศูนย์พร้อมกัน
เรียก ax + by = c
cx + dy = f
ว่าระบบสมการเชิงเส้นสองตัวแปรที่มีสองสมการ
คำตอบของระบบสมการคือค่าของ x และ y ที่ทำให้สมการทั้งสองสมการเป็นจริง

นักศึกษาคิดว่าคำตอบของระบบสมการเชิงเส้นมีเพียงคำตอบเดียวเสมอไปใช่หรือไม่ ให้ศึกษาตัวอย่างที่ 1 และ 2

ตัวอย่างที่ 1 กำหนดให้ x, y เป็นจำนวนจริงใด ๆ จงเขียนกราฟของระบบสมการเชิงเส้นสอง
ตัวแปรที่มีสองสมการดังต่อไปนี้บนแกนคู่เดียวกัน พร้อมทั้งหาคำตอบของสมการ
4x – 12y = 24 . . . . (1)
x – 3y = 6 . . . . (2)
วิธีทำ พิจารณาสมการที่ (2) จะพบว่าเมื่อนำ 4 ไปคูณทั้งสองข้างของสมการที่ (2) จะได้
ผลลัพธ์ (1) แสดงว่าเส้นตรงทั้งสองเส้นนี้เป็นเส้นตรงเดียวกัน
เขียนกราฟของสมการที่กำหนดได้ดังนี้

เส้นตรงทั้งสองเส้นนี้เป็นเส้นตรงเดียวกัน หรือกล่าวว่าเส้นตรงทั้งสองเส้นนี้ทับกัน คู่อันดับที่แทนจุดทุกจุดบนเส้นตรงคือคำตอบของระบบสมการเชิงเส้นที่กำหนดให้

ดังนั้นระบบนมการนี้มีคำตอบมากมาย

ตัวอย่างที่ 2 กำหนดให้ x, y เป็นจำนวนจริงใด ๆ จงเขียนกราฟของระบบสมการเชิงเส้นสอง
ตัวแปรที่มีสองสมการดังต่อไปนี้บนแกนคู่เดียวกัน พร้อมทั้งหาคำตอบของระบบสมการ
2x + 3y = 6 . . . . (1)
2x + 3y = 12 . . . . (2)
วิธีทำ เขียนกราฟของสมการที่กำหนดได้ดังนี้

จะเห็นว่าเส้นตรงที่ได้จากสมการ (1) และเส้นตรงที่ได้จากสมการ (2) ขนานกัน จึงไม่มีจุดตัด
นั่นคือระบบสมการเชิงเส้นสองตัวแปรนี้ไม่มีคำตอบ