สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ

สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ

สมบัติของจำนวนจริงเกี่ยวกับการบวก

          จำนวนตรรกยะ (rational number) เป็นจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์  และเขียนในรูปทศนิยมซ้ำได้จำนวนอตรรกยะ (irrational number)  เป็นจำนวนจริงที่ไม่ใช่จำนวนตรรกยะซึ่งไม่สามารถเขียนในรูปทศนิยมซ้ำหรือเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์แต่เขียนได้ในรูปทศนิยมไม่ซ้ำ และสามารถกำหนดค่าโดยประมาณได้การเขียนเศษส่วนในรูปทศนิยม คือ การนำส่วนไปหารเศษการเขียนทศนิยมในรูปเศษส่วน คือ ทศนิยม 1 ตำแหน่ง หารด้วย 10 2 ตำแหน่งหาร 100 ไปเรื่อยๆ แต่ถ้าเป็นทศนิยมซ้ำ ใช้วิธีลัด เช่น

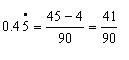
ตัวอย่าง  จงพิจารณาว่าจำนวนต่อไปนี้เป็นจำนวนชนิดใดโดยใส่เครื่องหมาย / ลงในช่องให้ถูกต้อง

สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ   มีดังนี้

1. สมบัติปิด

2. สมบัติการสลับที่

3. สมบัติการเปลี่ยนกลุ่ม

4. สมบัติการมีเอกลักษณ์

5. สมบัติการมีอินเวอร์ส

6. สมบัติการแจกแจง

สมบัติของจำนวนจริงเกี่ยวกับการบวก

                1.  สมบัติปิดของการบวก

ถ้า  a    R  และ b    R แล้ว  a  +  b    R

เช่น  ถ้า 4 , 5   R  แล้ว   4  +  5  =  9  ซึ่ง 9    R ด้วย

2.  สมบัติการสลับที่ของการบวก

ถ้า a    R  และ b    R แล้ว  a  +  b  =  b  +  a

เช่น  2  +  3  =  3  +  2

3.  สมบัติการเปลี่ยนหมู่สำหรับการบวก

ถ้า  a    R   ,  b    R   และ  c   R แล้ว  a  +  ( b +  c  )  =  (  a  +  b ) +  c

เช่น  2  +  ( 4  +  5 )  =  ( 2  +  4 )  +  5

4.  สมบัติการมีเอกลักษณ์การบวก

จำนวนจริงที่นำมาบวกกับจำนวนจริง  a  แล้วได้ผลลัพธ์เท่ากับ  a  เรียกจำนวนจริงที่นำมาบวกว่าเอกลักษณ์การบวก  ในระบบจำนวนจริงมีเอกลักษณ์การบวกจำนวนเดียว  คือ  0

เช่น  2  +  0  =  2  =  0  +  2

5.  สมบัติการมีอินเวอร์สของการบวก

จำนวนจริงที่บวกกับจำนวนจริง a  แล้วได้ผลลัพธ์เท่ากับ  0  คือ  –  a

เรียก  –  a  ว่าเป็นอินเวอร์สการบวกของ  a

เช่น  ( – 5 )  +  5  =  0  =  5  +  ( – 5)

สมบัติของจำนวนจริงเกี่ยวกับการคูณ

                1.  สมบัติปิดของการคูณ

ถ้า  a    R  และ b    R แล้ว  a    b    R

เช่น   3   R  แล้ว   4    R  แล้ว  3    4  =  12  ซึ่ง  12     R

2.  สมบัติการสลับที่ของการคูณ

ถ้า a   และ b    R แล้ว  a   b  =  b    a

เช่น  2    R  และ  3    R  แล้ว  2   3  =   3    2

3.  สมบัติการเปลี่ยนหมู่สำหรับการคูณ

ถ้า  a  ,  b  และ  c    R  แล้ว   ( ab ) c    =   a  ( b c )

เช่น  2 , 3  และ  4    R  แล้ว  ( 2 3 ) 4   =   2    ( 3 4 )

4.  สมบัติการมีเอกลักษณ์การคูณ

จำนวนจริงที่นำมาคูณกับจำนวนจริง  a  แล้วได้ผลลัพธ์เท่ากับ  a  เรียกจำนวนจริงที่นำมาคูณว่าเอกลักษณ์การคูณ  ในระบบจำนวนจริงมีเอกลักษณ์การคูณจำนวนเดียว  คือ  1

เช่น  1 3  =  3   =   3 1

5.  สมบัติการมีอินเวอร์สของการคูณ

จำนวนที่คูณกับจำนวนจริง a  แล้วได้ผลลัพธ์เป็น  1  คือ    a^{– 1}  เรียก  a^{– 1} ว่าเป็นอินเวอร์สการคูณของจำนวนจริง  a

เช่น  4   4 ^{– 1}  =  4       =    =  1  ดังนั้น  4 ^{– 1}  หรือ    เป็นอินเวอร์สการคูณของ 4

หรือ  4   4 ^{– 1}  =     4 ^{1 +( -1 )}  =  4 ⁰  =  1

ตัวอย่างของอินเวอร์สการบวกของจำนวนจริง

1.  อินเวอร์สการบวกของ     5            คือ      – 5

2.  อินเวอร์สการบวกของ    0.3       คือ     – 0.3