สรุปเนื้อหาเรื่องกราฟของฟังก์ชันกำลังสอง(พาราโบลา) ม.3
ฟังก์กำลังสอง
ฟังก์ชันกำลังสอง (Quadratic function)
ฟังก์ชันกำลังสองเป็นฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a, b, c เป็นจำนวนจริงใด ๆ และ a¹ 0 ซึ่งกราฟของ
ฟังก์ชันกำลังสอง เรียกว่า พาราโบลา
1) y = 2x2 + 3x – 10 เมื่อ a = 2 , b = 3 และ c = -1
2) y = x2 + 1 เมื่อ a = 1 , b = 0 และ c = 1
3) y = -x2 + 2x + 1 เมื่อ a = -1 , b = 2 และ c = 1
1) กราฟของฟังก์ชันกำลังสอง ที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0
2) กราฟที่กำหนดด้วยสมการ y = ax2 + k เมื่อ a ¹ 0 และ k ¹ 0
กราฟที่กำหนดด้วยสมการ y = ax2 + k เมื่อ a ¹ 0 และ k ¹ 0 จะเป็นกราฟพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุด อยู่ที่ (0, k) และแกนสมมาตรคือ แกน Y
3. กราฟของ y = a(x – h)2 เมื่อ a ¹ 0 และ h > 0
3.1) กราฟที่กำหนดด้วยสมการ y = a(x – h)2 เมื่อ a ¹ 0 และ h ¹ 0 จะเป็นกราฟ
พาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุดอยู่ที่ (h, 0) และแกนสมมาตรคือเส้นตรง x = h
3.2) กราฟของ y = a(x – h)2 เมื่อ a ¹ 0 และ h < 0
ถ้า h < 0 จะได้สมการใหม่เป็น y = a(x – (-h))2
= a(x + h)2
4. กราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ y = a(x – h)2 + k เมื่อ a ¹ 0 , h ¹ 0 และ k ¹ 0 จะเป็นพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุดอยู่ที่ (h, k) และมีแกนสมมาตรคือ เส้นตรง x = h
5. กราฟที่กำหนดด้วยสมการ y = ax2 + bx + c เมื่อ a ¹ 0 การเขียนกราฟควรจัดสมการให้อยู่ในรูป
y = a(x – h)2 + k จะทำให้เขียนกราฟได้ง่ายขึ้น
จากสมการ y = ax2 + bx + c สามารถเปลี่ยนให้อยู่ในรูป y = a(x – h)2 + k ได้โดยใช้ความรู้เรื่องกำลังสองสมบูรณ์
ฟังก์ชันกำลังสอง(Quadratic function)
ฟังก์ชันพีชคณิตที่มีตัวแปรต้นกำลังศูนย์หรือหนึ่งนั้นเป็นฟังก์ชันเชิงเส้น นอกเหนือจากนี้จะให้กราฟที่มีลักษณะเป็นเส้นโค้งในที่นี้เราจะศึกษาฟังก์ชันที่อยู่ในรูปของพหุนามกำลังสอง
ฟังก์ชันกำลังสองเป็นฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a, b, c เป็นจำนวนจริงใด ๆ และ a ¹ 0 ซึ่งกราฟของฟังก์ชันกำลังสอง เรียกว่า พาราโบลา
1) y = 2x2 + 3x – 10 เมื่อ a = 2 , b = 3 และ c = -1
2) y = x2 + 1 เมื่อ a = 1 , b = 0 และ c = 1
3) y = -x2 + 2x + 1 เมื่อ a = -1 , b = 2 และ c = 1
1) กราฟของฟังก์ชันกำลังสอง ที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0
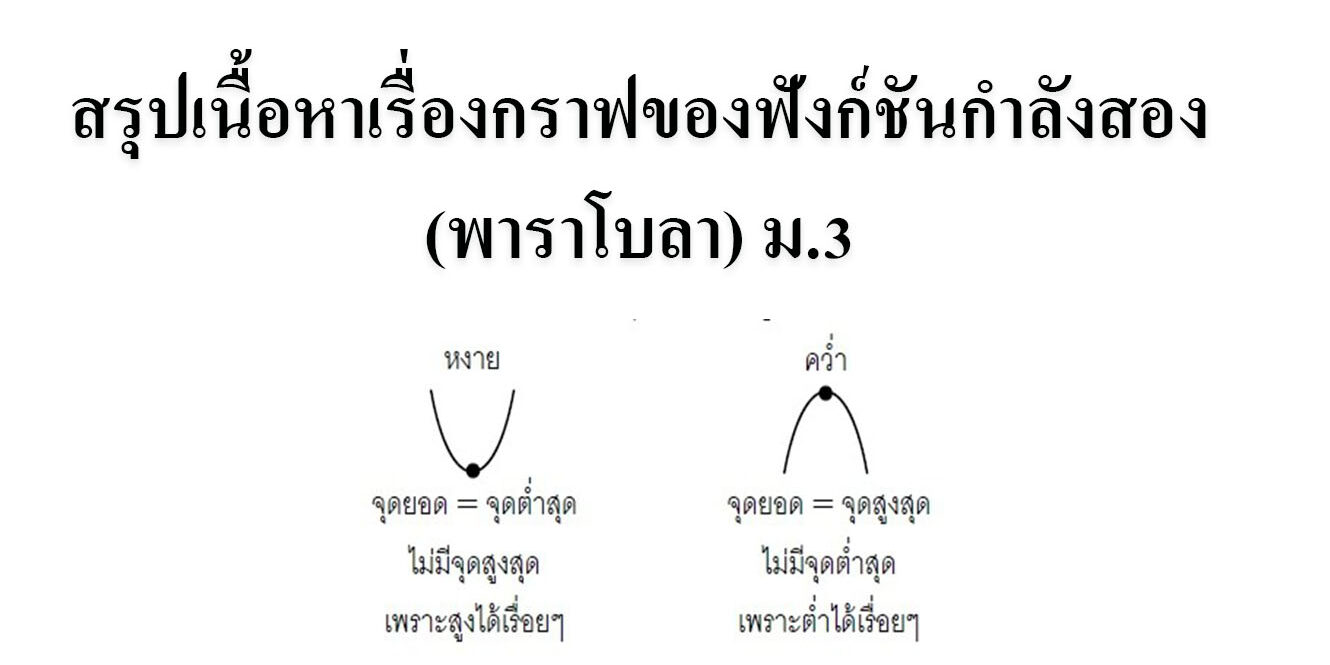
กราฟของฟังก์ชันกำลังสอง มีชื่อเรียกว่า พาราโบลา ซึ่งลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ a , b และ c และเมื่อ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ และกราฟของฟังก์ชันกำลังสองที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0 เมื่อ a > 0 และชนิดคว่ำ เมื่อ a < 0
สรุป ลักษณะของกราฟที่กำหนดด้วยสมการ y = ax2 เมื่อ a ¹ 0
! เมื่อ a > 0 ได้พาราโบลาหงาย จุดต่ำสุดอยู่ที่ (0, 0)
เมื่อ a < 0 ได้พาราโบลาคว่ำ จุดสูงสุดอยู่ที่ (0, 0)
! แกนสมมาตรคือ แกน Y หรือเส้นตรง X = 0 ,
สมการแกนสมมาตรคือ X = 0
! เมื่อ a > 0 ค่าต่ำสุดคือ 0 และ เมื่อ a < 0 ค่าสูงสุดคือ 0
! | a | ยิ่งมากกราฟยิ่งแคบ
2) กราฟที่กำหนดด้วยสมการ y = ax2 + k เมื่อ a ¹ 0 และ k ¹ 0
กราฟที่กำหนดด้วยสมการ y = ax2 + k เมื่อ a ¹ 0 และ k ¹ 0 จะเป็นกราฟพาราโบลาที่มีจุดวกกลับหรือจุดสูงสุดหรือจุดต่ำสุด อยู่ที่ (0, k) และแกนสมมาตรคือ แกน Y
กราฟฟังก์ชันกำลังสอง
พหุนามกำลังสองอยู่ในรูปของ ax2 + bx + c เมื่อ a, b และ c เป็นจำนวนจริงใด ๆ เรานิยามเป็นฟังก์ชัน
P(x) = ax2 + bx + c
= a[(x + b/(2a))2 – b2/(4a2) + c/a]
= a[(x + b/(2a))2 – (b2 – 4ac)/(4a2)]
ถ้ากำหนดให้ h = – b/2a และ k = – (b2 – 4ac)/(4a) ฟังก์ชันที่อยู่รูป
P(x) = a(x – h)2 + k
มีกราฟเป็นรูปพาราโบลา
กรณีที่ a > 0 จะเป็นกราฟพาราโบลาหงายและมีต่ำสุดอยู่ที่จุด (h,k)
กรณีที่ a < 0 จะเป็นกราฟพาราโบลาคว่ำมีจุดสูงสุดอยู่ที่จุด (h,k)
ฟังก์ชันกำลังสอง
กราฟฟังก์ชันกำลังสอง
พหุนามกำลังสองอยู่ในรูปของ ax2 + bx + c เมื่อ a, b และ c เป็นจำนวนจริงใด ๆ เรานิยามเป็นฟังก์ชัน
P(x) = ax2 + bx + c
= a[(x + b/(2a))2 – b2/(4a2) + c/a]
= a[(x + b/(2a))2 – (b2 – 4ac)/(4a2)]
ถ้ากำหนดให้ h = – b/2a และ k = – (b2 – 4ac)/(4a) ฟังก์ชันที่อยู่รูป
P(x) = a(x – h)2 + k
มีกราฟเป็นรูปพาราโบลา
กรณีที่ a > 0 จะเป็นกราฟพาราโบลาหงายและมีต่ำสุดอยู่ที่จุด (h,k)
กรณีที่ a < 0 จะเป็นกราฟพาราโบลาคว่ำมีจุดสูงสุดอยู่ที่จุด (h,k)
ฟังก์ชันกำลังสอง
เช่น
𝑓(𝑥) = 2𝑥2− 𝑥 + 5 → 𝑎 = 2 , 𝑏 = −1 , 𝑐 = 5
𝑓(𝑥) = 3 + 2𝑥 − 𝑥2 → 𝑎 = −1 , 𝑏 = 2 , 𝑐 = 3
𝑓(𝑥) = 𝑥2 → 𝑎 = 1 , 𝑏 = 0 , 𝑐 = 0
ถ้านำฟังก์ชันกาลังสอง ไปวาดกราฟ จะได้กราฟที่เรียก ว่า “พาราโบลา” ซึ่งจะมีลักษณะเป็นเส้นโค้งที่มีการวกกลับ


ถ้า 𝑎 เป็นบวก จะได้พาราโบลา “หงาย”
ถ้า 𝑎 เป็นลบ จะได้พาราโบลา “ควา”
จุดที่พาราโบลา วกกลับ เรียกวา “จุดยอด” สูตรหาพิกดของจดยอด คือ (− 𝑏 , 4𝑎𝑐−𝑏 )
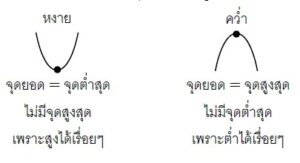
เรียกแนวเส้นตรงที่ผ่ากลางพาราโบลาว่า “แกนสมมาตร”
เวลาตอบแกนสมมาตร ให้ตอบเป็นสมการ 𝑥 = − 𝑏ส่วน 2a

= พิกัดตัวหน้าของจุดยอด
ตัวอย่าง จงวาดกราฟของฟังกชน 𝑓(𝑥) = 𝑥2+ 2𝑥 − 5 พร้อมทั้งบอกสมการแกนสมมาตร
วิธทำ จะได้ 𝑎 = 1 , 𝑏 = 2 , 𝑐 = −5
เนื่องจาก 𝑎 = 1 เป็นบวก ดังนั้น เป็นกราฟหงาย

จุดยอด เป็นจุดต่ำสุด และมีพิกัด = (− 𝑏 , 4𝑎𝑐−𝑏 )
= (− 2 , 4(1)(−5)−2 )
= (−1 , −24)
= (−1 , −6)
สมการแกนสมมาตร คือ 𝑥 = −1
นรูป 𝑓(𝑥) = 𝑎𝑥2+ 𝑏𝑥 + 𝑐 เมื่อ 𝑎, 𝑏, 𝑐 เป็นตัวเลขอะไรก็ได้ ที่ 𝑎 ≠ 0
เช่น
𝑓(𝑥) = 2𝑥2− 𝑥 + 5 → 𝑎 = 2 , 𝑏 = −1 , 𝑐 = 5
𝑓(𝑥) = 3 + 2𝑥 − 𝑥2 → 𝑎 = −1 , 𝑏 = 2 , 𝑐 = 3
𝑓(𝑥) = 𝑥2 → 𝑎 = 1 , 𝑏 = 0 , 𝑐 = 0
ถ้านำฟังก์ชันกาลังสอง ไปวาดกราฟ จะได้กราฟที่เรียก ว่า “พาราโบลา” ซึ่งจะมีลักษณะเป็นเส้นโค้งที่มีการวกกลับ


ถ้า 𝑎 เป็นบวก จะได้พาราโบลา “หงาย”
ถ้า 𝑎 เป็นลบ จะได้พาราโบลา “ควา”
จุดที่พาราโบลา วกกลับ เรียกวา “จุดยอด” สูตรหาพิกดของจดยอด คือ (− 𝑏 , 4𝑎𝑐−𝑏 )
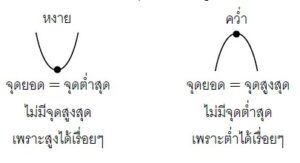
เรียกแนวเส้นตรงที่ผ่ากลางพาราโบลาว่า “แกนสมมาตร”
เวลาตอบแกนสมมาตร ให้ตอบเป็นสมการ 𝑥 = − 𝑏ส่วน 2a

= พิกัดตัวหน้าของจุดยอด
ตัวอย่าง จงวาดกราฟของฟังกชน 𝑓(𝑥) = 𝑥2+ 2𝑥 − 5 พร้อมทั้งบอกสมการแกนสมมาตร
วิธทำ จะได้ 𝑎 = 1 , 𝑏 = 2 , 𝑐 = −5
เนื่องจาก 𝑎 = 1 เป็นบวก ดังนั้น เป็นกราฟหงาย
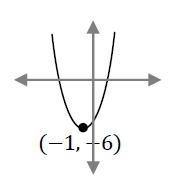
จุดยอด เป็นจุดต่ำสุด และมีพิกัด = (− 𝑏 , 4𝑎𝑐−𝑏 )
= (− 2 , 4(1)(−5)−2 )
= (−1 , −24)
= (−1 , −6)
สมการแกนสมมาตร คือ 𝑥 = −1