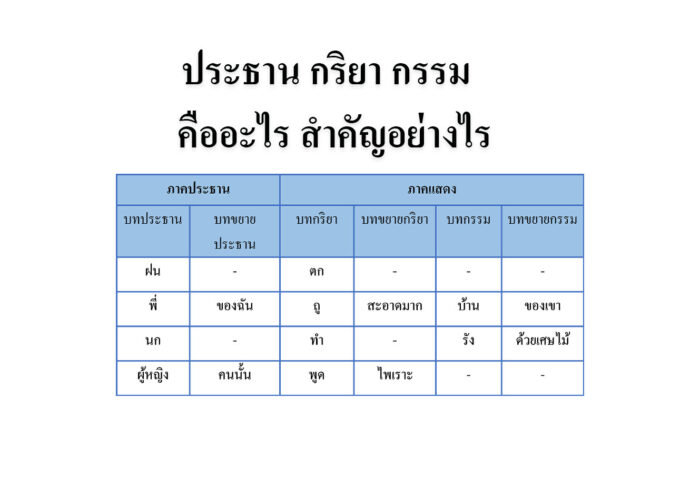
การเปลี่ยนแปลงสภาพภูมิอากาศ
การเปลี่ยนแปลงสภาพภูมิอากาศ ผลกระทบจากการเปลี่ยนแปลงสภาพภูมิอากาศ และภาวะโลกร้อน น้ำทะเลอุ่นขึ้น: ภาวะโลกร้อนส่งผลให้มหาสมุทรดูดซับความร้อนส่วนเกินเกือบ 90% จากอากาศโดยรอบ ทำให้น้ำทะเลอุ่นขึ้น แม้ว่าความร้อนส่วนใหญ่จะถูกดูดซับในพื้นผิว แต่เนื่องจากอัตราการให้ความร้อนเพิ่มขึ้น ความร้อนจึงเข้าถึงน้ำทะเลในระดับลึกได้ นอกจากนี้มหาสมุทรที่อุ่นขึ้นอาจนำไปสู่การเกิดพายุที่รุนแรงขึ้น และการเพิ่มขึ้นของระดับน้ำทะเล ได้ส่งผลกระทบต่อระบบนิเวศของแนวปะการัง การเจริญเติบโตของพืชทะเล และกระทบต่อการอยู่รอดของสัตว์ทะเล