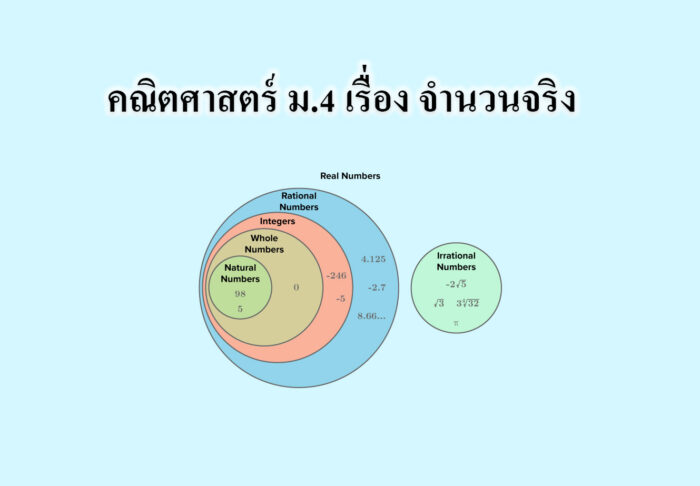
คณิตศาสตร์ ม.4 – เซต
คณิตศาสตร์ ม.4 – เซต สัญลักษณ์ { } แทน เซต ∈ แทน คำว่า” เป็นสมาชิก” ∉ แทนคำว่า “ไม่เป็นสมาชิก” ⊂ แทนคำว่า “สับเซต” ⊄ แทนคำว่า ” ไม่เป็นสับเซต” การนับจำนวนสมาชิกในเซต จำนวนสมาชิกของเซต A เขียนแทนด้วย n(A) ถ้าสมาชิกในเซตซ้ำกันให้เขียนเพียงครั้งเดียว ชนิดของเซต เซตจำกัด คือ เซตที่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว เซตอนันต์ คือ เซตที่ไม่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว เซตว่าง คือ เซตที่ไม่มีสมาชิกในเซตเลย หรือเขียนแทนด้วย ∅ เอกภพสัมพัทธ์ (U) คือ เซตที่กำหนดขอบเขตสิ่งที่เรากำลังพิจารณา ความสัมพันธ์ระหว่างเซต เซตที่เท่ากัน คือ เซตที่สมาชิกทุกตัวเหมือนกัน ถ้าเซต A เท่ากับเซต B จะเขียนแทนด้วยสัญลักษณ์ A…